7:方程式解法が楽な問題の実例 2016 女子学院
方程式さえ知っていれば解けてしまう
「方程式そのまんまで解けるし、しかもその解法が最も簡単という問題が出題されている」
実例を見てみましょう。
2016年 女子学院 の大問6(最後の問題)です。
※ちなみにこの問題は出題時、ミス(数値ミス)がありました。後で詳しくかきます。
下は数値ミスなしバージョンです、安心して解いてみて下さい。
あるクラス30人の生徒の通学時間を調べたら、次のことがわかりました。
25分以上の通学時間の生徒の平均は、58分
25分未満の通学時間の生徒の平均は、24分
60分以上の通学時間の生徒の平均は、65分
60分未満の通学時間の生徒の平均は、27分
25分以上60分未満の生徒の人数は5人
通学時間が60分以上の生徒の人数は□人で、クラス全員の通学時間の平均は□分□秒です。
さあ、まずはとにかくこの問題を解いてみてください。
もちろん方程式を使っていただいてかまいません。
通学時間
25分未満 X(人)
25分以上60分未満 5(人)
60分以上 Y(人)
とします。
もちろん、
X+Y=25・・・①
です。
それぞれのカテゴリの、通学時間の合計(平均時間×人数)をだすと、
25分以上の通学時間の生徒の合計は、 58(5+Y)
25分未満の通学時間の生徒の合計は、 24X
60分以上の通学時間の生徒の合計は、 65Y
60分未満の通学時間の生徒の合計は、 27(5+X)
全生徒の通学時間の合計について、等式がかけます。
58(5+Y)+24X=65Y+27(5+X)
これを整理すると、
3X+7Y=155
となり、①式と連立して、
Y=20(人)を得ます。
よって、X=5人 Y=20人 なので、
よってクラス全員の通学時間の平均は
(25×58+5×24)÷30=52分20秒
いかがでしたでしょうか。
ただの連立方程式!!!です。
「難関校では、連立方程式さえ知っていれば容易に解けるような類の
問題は出題されない」
という噂話は、必ずしも真実ではないことがお分かりいただけたと思います。
算数的視点でこの問題を解くと
もしこの問題を算数的に解こうとするとどうなるのか、お見せします。
何をもって算数的解法なのかも曖昧ですが、少なくともガンガン消去算を使うと上と同じ解法になるので使わない方向で解きます。
注 平均といえば面積図、算数の常識ですが、算数の素養がないとよくわからないと思います。算数的解法は「なんだか難しそうだな」とわかってもらうことが目的ですので、この部分を読み飛ばしていただいても構いません。
面積図にまとめると下図のようになります。
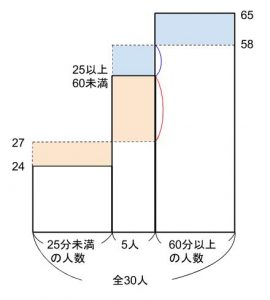
水色の面積が等しいため、青い長さは7の倍数です。
オレンジの面積が等しいため、赤い長さは3の倍数です。
よって、
7の倍数+3の倍数=31(58-27)
これを満たすのは、
28+3=31
7+24=31
のどちらかです。
28+3=31 のときに、条件通りになり、これで解決します。
7+24=31のとき、25分未満の人が40人となり、条件に合いません。
いかがでしたか。
結構高級な思考力を要しますね。
この問題は
連立方程式を知っていれば圧倒的に有利
は間違いありません。
このような出題をしてくる以上、中学校側も
そのような生徒を歓迎するという意向なのでしょう。
(もちろん方程式とは相入れないような類の問題を数多くだす学校もあります。入試問題はどのような生徒が欲しいかを示すメッセージです。ちなみにこれは国語や社会で、より顕著です。”思想”に関わる部分ですので、保護者様はよく問題を吟味されることをオススメいたします。)
方程式解法を模範解答としていかことが、出題ミスから分かる
ちなみにこの問題は実入試においては、不完全な問題として出題されました。
いわゆる出題ミスで、全受験生得点という処置がされました。
具体的には、以下の赤字部分です。ここだけ、先の問題と違います。
この数値では問題として壊れています。
あるクラス30人の生徒の通学時間を調べたら、次のことがわかりました。
50分以上の通学時間の生徒の平均は、58分
50分未満の通学時間の生徒の平均は、24分
60分以上の通学時間の生徒の平均は、65分
60分未満の通学時間の生徒の平均は、27分
50分以上60分未満の生徒の人数は5人
通学時間が60分以上の生徒の人数は□人で、クラス全員の通学時間の平均は□分□秒です。
これを先と同じように連立方程式で解くと、出題ミスにはまったく気づくことなく方程式が解けて先の答えと同じものを得ます。
一方面積図で考察すると、この問題が不成立であることはすぐに気付けます。
先の面積図(25分部分を50分に変えて)での青い長さは7で確定し、その結果、50分未満の生徒の人数が40人となります。
これでは条件にあいません。問題のような状況は実際には不可能であることがわかります。
このことからも、女子学院の数学の先生たちが、連立方程式で解くことを想定して問題作成をしていることがうかがえます。
ちなみに、入試問題の不備はたいていは塾業界の先生たちが解くことで見つけられ、学校に報告され、それを受けて学校側が対応を発表します。算数以外の科目でもよくある話です。

