1:線分図から式処理への入り口
消去算は、今後ありとあらゆる問題で必要になる計算技術です。大人の目から見れば連立方程式です。小学生が方程式をやるのです。中学受験においては、必須であると知っておいてください。
ただし1点大きな違いがあります。それは、小学生は「負の数」を扱わないということです。それゆえに、教え方に繊細さが求められます。
逆に言えば、負の数もふくめて、すべてを小学生に教えてしまえ!という方法論もないわけではありません・・・
当サイトでは、一般的な大手進学塾と同様に、負の数を真正面から扱うことはしません。
小学生にとって理解のしやすい指導法をとります。
1:線分図から式処理へ
例題1
りんご1個の値段は、みかん3個の値段と同じです。りんご2個とみかん1個の合計金額が280円のとき、りんご1個の値段はいくらですか。
解説

今日はこんな問題ですが・・

これは新しい問題じゃないですね。多分1人で解けますよ!
3倍は線分図であらわせるから!
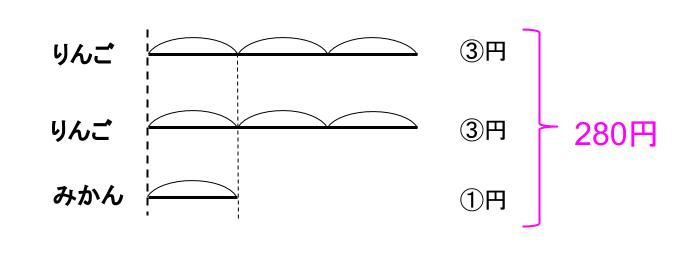

合計は280円
つまり、⑦=280
①=40
だから、リンゴは③だから、120円!!カンペキですね!!

うん、今までの学習がきちんと身についているようで素晴らしいよ。
ところで、今回の例題が下のようだったらどうかな。同じ仕組みの問題なんだけど、個数が多くなっているよ。
例題2
りんご1個の値段は、みかん3個の値段と同じです。りんご20個とみかん15個の合計金額が3000円のとき、りんご1個の値段はいくらですか。
解説

リンゴの線分図を20本、ミカンの線分図を15本かくのは嫌ですね・・・

そうだね。ところで、リンゴ1個の値段は③円、ミカン1個の値段は①円は、線分図をかかなくてもいいよね?

え?どういうこと?

そもそも、線分図だってちょうど3倍の図をかかなくなっているよね。③や①という便利な表記法のおかげで。
③円が2個あれは、⑥円になるのも、線分図をかかなくてもわかるでしょ。

あ、そうか。では
リンゴが20個で、③×20=〇60
ミカンが15個で、①×15=〇15
合計が〇75=3000円 だから、①=40円だ!!

その通り。必ずしも線分図でなくても良いことがわかったね。

もう線分図はかかなくていいですか?

いいや、どんどんかいていくべきだよ。
もちろん20本も線分図をかくようなことはしなくていいのだけれど。
図は、問題の整理のためにかいていくべきなんだ。
「かいてはダメ」でもないし
「かかないとダメ」でもない。
問題をすっきりと解くための「手段」が図をかくことなんだ。
あたりまえすぎて省略できる図をいちいちかかなくもいいけど、どうやって解いていいいのかわからない問題を解く時に、図をかかないのは最悪だ。

わからないときは図をかけってことですかね。

そうなんだけど、どんなときも書く、くらいでちょうど良いよ。特に初心者のうちはどんどん図をかかないとダメだ。そうやって問題の仕組みにふれていくうちに、いずれ図を省略して解くことができるようになる。
でも、図を省略することがエライわけではないからね。
それに、難関校の入試問題ともなれば、図を省略して解くなんて絶対に無理だ。図をかいて整理することそのものを練習しておく必要があるよ。

とにかく図が大事なんですね。はい。
