線分図を積極的に利用したいパターン
- 例題1
- ある本を、1日目に全体の \(\displaystyle \frac{1}{4}\) を読み、2日目に残りの \(\displaystyle \frac{3}{5}\) を読んだところ、残りは60ページだった。この本は全部で何ページありますか。
- 解説
-

えーっと、\(\displaystyle \frac{1}{4}×\displaystyle \frac{3}{5}=\displaystyle \frac{3}{20}\)
全ページが⑳なら残りは、③③=60ページかな・・・

あれれ、大間違いだな。
よくわからないままに計算しちゃだめだよ。
よくわからないってことはないんですけど・・・
多分わかります。
自分がわかっているのかわからないのかさえもわからないんだね。
とにかく算数は「ていねいさ」が非常に大切だ。
途中で1か所でも間違ったら、それ以降すべて間違いが連鎖するよ。
”絶対にここまでは正しい。”という絶対に正しい、絶対にわかっている、という階段を1つ1つ上っていかないとだめだよ。まずは線分図にしてみてみよう。

はい。
えっと、下図のようになりますね。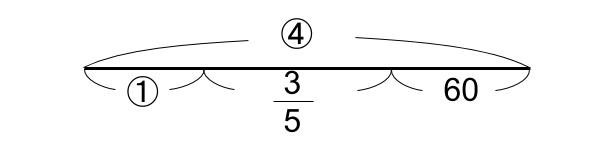

この図は間違っているわけじゃないけど・・・100点満点の図とは言えないかな。
もしかしたら、学くんはもう完璧にわかっていて、もうこの問題を正しく解けるのかもしれないけどさ・・・。
どうせ図をかくのなら、他の人が見てもわかるレベルの図をかくように心がけて欲しいな。
問題文を読まなくたって、図をみればどんな状況なのかわかるような図をかけるように練習していかないといけないよ。
この図では他の人が見ても、わからないということですか?

うん、わからない。他の人っていうのは、1か月後の学くんでもある。
1か月後に見たらわからないよ。
どこがダメなのか教えるよ、\(\displaystyle \frac{3}{5}\) の所だ。これは比なんだよ。
比っていうことは、2つのものを比べているわけだ。この線分図だと、何が3で何が5にあたるのかわからない。
そして、それを深く考えないでわからないまま、なんとなく計算だけして間違う子も実は非常に多いんだよ。

①読んだあとの残りが5です。
図をかきなおしました!下図です。
どうですか?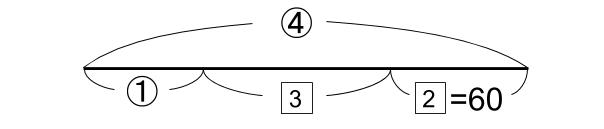

うん、とてもいいね。この図なら誰が見ても状況を間違えることはないね。

2=60だから、
5=150
これは、③でもある。③=150なので、
④=200この本は200ページあります!

はい、正解です!
ところで、今かいた図なんだけども、下のように、線分図を2段に書くやり方もあるよ。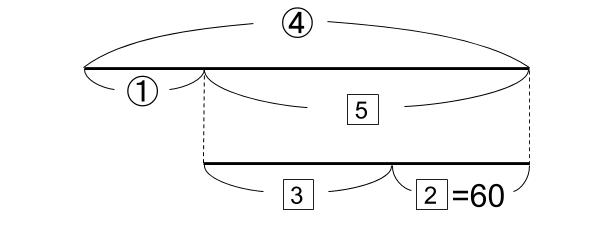

1つの線分図に情報をたくさん書いていくと、ごちゃごちゃになってわかりづらくなる。
それを避けるための書き方だよ。より複雑な問題に対応するためには、このような書き方もあると知っておいてね。
例えば、
3日目に残りの \(\displaystyle \frac{1}{5}\) を読み、4日目に残りの \(\displaystyle \frac{1}{2}\) 読んだら・・・このように、さらに話が続いていく問題には、下に線分図を書き足していくやり方が絶対におススメだよ。

なるほど~
保護者さまへ式だけで処理しても構いません。
上図のような状況がきちんとわかっていれば、もちろん計算一発で出してもかまいませんが、線分図を書く練習は絶対にしておくべきです。
そもそも、正しい計算式を導くために、状況整理が必要ならば図示をするのです。

ちなみにこの例題は、分数のかけ算を連続するだけでも解けるよ。
あるいは、連比で解くこともできるよ。
いろんな解き方がありますね。
おススメの解き方はありますか?線分図をかくことが最もおすすめです。
問題の状況全体を把握することが最大の重要事項だからです。
状況把握ができてこそ、その後の計算処理につながるんだからね。例えば連比の解法は、その計算処理のやり方の1つにすぎません。
状況把握ができない状態では、何をどう計算していいのか迷子になるだけだからね。逆に言えば、問題の状況全体が把握できてさえいれば、どのような計算処理で解いたって自由なのです。
