ニュートン算の標準問題
- 例題7
-
水そうに一定の割合で水が注がれ続けています。満水から、ポンプ7台で水をくみだしはじめました。
くみだしはじめてから30分後に2台のポンプが壊れたのですが、残ったポンプ5台で最後まで水をくみ出したところ、くみだしはじめてから45分後に空になりました。
また、2台のポンプが壊れたとき、水そう内の水量は満水の \(\displaystyle \frac{1}{4}\) でした。
この水そうを、満水から空になるまでポンプ11台でくみだすならば、何分で空になりますか。
- 解説
-

えっと・・・かなり複雑ですね。

そうでもないよ。
とにかく情報整理をしてみようね。
はじめの30分は、ポンプ7台で \(\displaystyle \frac{3}{4}\) をくみだした。
次の15分は、 ポンプ5台で \(\displaystyle \frac{1}{4}\) をくみだした。
「水が注がれている」というじゃまがいつも通りある。
\(\displaystyle \frac{3}{4}\) ÷(⑦-じゃま)=30分
\(\displaystyle \frac{1}{4}\) ÷(⑤-じゃま)=15分
これでいいのかな・・・

はい。
とてもうまくいってますよ。仕事量は、\(\displaystyle \frac{3}{4}\) や \(\displaystyle \frac{1}{4}\) のままでも解けるけど、もっと計算が楽になりそうな数値にするのがおススメかな。
仕事算なんでね。

えっと・・・何がいいかな・・・
90と30にします。
満水が120です。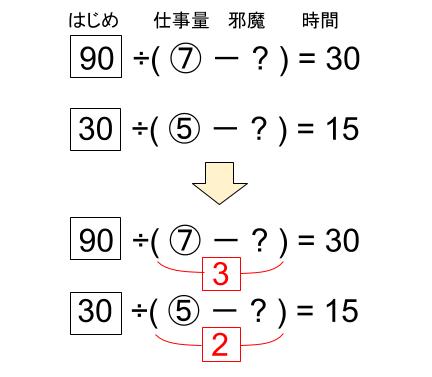

⑦-?=3
⑤-?=22つの式の差をとって、
②=1つまり、下図のようになる。
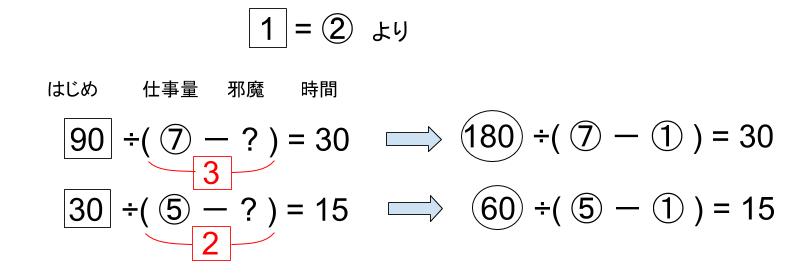

うまくいってますね。
最後の仕事算をすれば終了ですね。
はじめから最後まで11台でくみだす。
つまり、満水120は◯240なので、
〇240÷(⑪-①)=24(分)求まりました!
24分で空になります。
正解です!よく理解できているね。
