ニュートン算の標準問題
- 例題4-1
-
水そうに水が入っていて、毎分一定量の水が流入しています。ポンプ4台でくみだすと20分で空になり、ポンプ9台でくみだすと8分で空になります。
はじめに水そうに入っていた水の量は何Lですか。ただしポンプは1台で毎分9Lの水をくみ出すことができます。
- 解説
-

さっきの問題と似てますね。

似ているんだから、似たように解いてみればいいよ。
もし何か違っていたら、そのときその場で考えれば大丈夫。
ポンプ4台は1分で、9×4=36(L)
ポンプ9台は1分で、9×9=81(L)
仕事をする。
毎分流入してくる水がじゃまですね。つまり、
はじめ÷(36L-じゃま)=20分
はじめ÷(81L-じゃま)=8分ということで、はじめの仕事量=80とおきます。
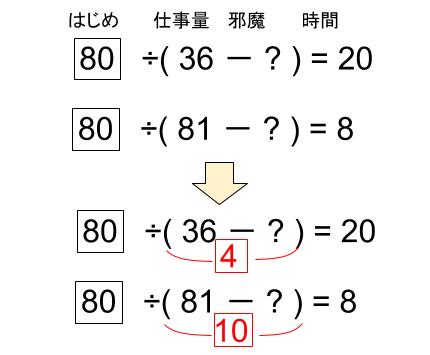

36L-じゃま=4
81L-じゃま=10
2つの式の差をとって、6=45L、3で割って、2=15Lであることがわかります。よって、はじめに入っていた量は、80=600L
求まりました。
600Lです。

正解です。
ところで、さっきの問題と今回の問題は何が違ったと思う?
ポンプのくみ出す具体的な量が9Lと与えられています。

そうだね。
実はさっきの問題よりも、この問題の方が与えられている情報が多かったんだよ。
情報が他にあろうがなかろうが、とにかくニュートン算は先生が教えたまとめ方1つで必ずうまくいくからね。もちろん別解もあるのだけれど、まずは1つ、得意な形をしっかり固めようね。
余裕ができたら別解にも手をのばしていけばいいよ。
- 例題4-2
-
ある美術館に、毎分10人ずつの人が来館していますが、午後2時の時点で入館待ちの行列ができています。3か所の受付で入場させていくと行列は30分でなくなり、5か所の受付で入場させていくと行列は14分でなくなります。
午後2時の時点で並んでいた人は何人ですか。
- 解説
-

お!水そうじゃないですね。

はい。水そうではないけど、ニュートン算であることがわかりますね。
じゃまのある仕事算ならば、ニュートン算です。さて、今度は「じゃま」の値が与えられている問題だ。
毎分10人ずつの人が来館する。
これも普通に教えた通りにやるだけだってことを確認してくださいね。
3か所の受付が1分で減らす人数を③、
5か所の受付が1分で減らす人数を⑤とすると、はじめ÷(③-10人)=30分
はじめ÷(⑤-10人)=14分
はじめは、30と14の最小公倍数である210とします。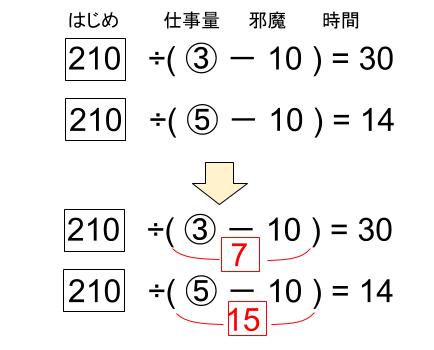

③-10=7
⑤-10=152つの式の差をとって、②=8、2で割って、①=4であることがわかります。
③-10=7
なので、③=12を入れて、
12-10=7より、5=10人
午後2時に並んでいた人は、210=420人
求まりました。
420人です。
正解です!
とにかくたった1つのやり方であらゆるパターンが解決できるということを学んでくださいね!保護者さまへ行列のニュートン算は、厳密に考察すると、答えが変化するものもあります。グラフで考えた場合、一直線のグラフにならず、階段状のグラフになるからです。しかし、このことに目をつぶって解くことが受験算数の世界では暗黙のルールとなっているようなところがあります。
