- 例題2
-
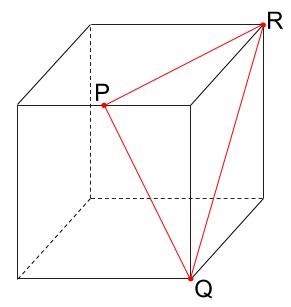
下の図は、1辺の長さが12cmの立方体です。点Pは辺の真ん中の点です。この立方体を3点P、Q、Rを通る平面で切断します。その切断面を作図しなさい。また、切断面の図形の名前を答えなさい。
- 解説
-

この問題は、こうなるかな。
これでいいのかな?
はい、正解です。
この問題は、3点P、Q、Rを結ぶだけでOKなのです。
「立体の切断面の切り口の作図」ルール
1.同じ平面上の点は結ぶ。
2.平行な面には、平行な線を引くのうち、ルール1だけで作図が完成したということなのです。
ルール2は使いませんでした。
なんか、簡単すぎて不安になっちゃいましたよ。

ところで、切断面の図形の名前は何でしょうか?

三角形ですね・・・

三角形の中でも
「直角三角形」
「二等辺三角形」
「直角二等辺三角形」
「正三角形」
この4つにあてはまるのかどうか、これについて考えないといけないね。
もちろんどれにもあてはまらないときは「三角形」で正解なんだけどね。
わからないけど、直角二等辺三角形かも・・・
点Pのところが直角で。
これはなかなか難しい問題なんだよね。
答えはね、二等辺三角形です。
PQとPRの長さが等しい二等辺三角形だ。
点Pのところの角は、直角ではないんだ。これらについて説明していくね。

まずは、PQとPRの長さが等しいことから見ておこう。
下図の色をつけた直角三角形が合同だからです。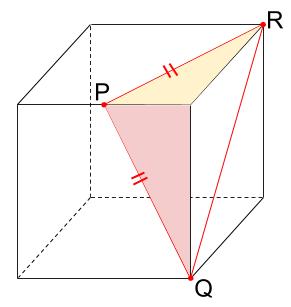

なるほど!
なんとなく同じ長さかなって思ったけど、確かに同じですね。
次に、点Pのところの角が直角ではないことの説明だ。
下図の左の切断面が長方形で、このとき点Pのところの角が直角になるよね。
今回の図形では、直角より小さいことがわかる。
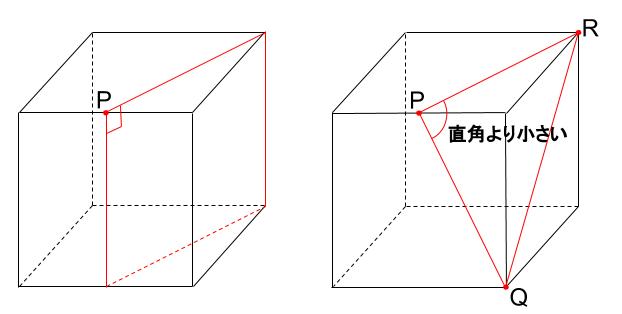

わかったような・・・わからないような・・・

とりあえず、
「立方体の切断では、切断面に直角三角形は絶対にできない」
と暗記しておきましょうかね。小学生はそれでOKですよ。