仕事をする人が2種類のパターン
- 例題2
- ある仕事をするのに、大人6人が7時間仕事をすれば終わります。この仕事は、子ども15人で4時間仕事をすることでも終わります。この仕事を大人7人、子ども2人ですると終わらせるのに何時間かかりますか。
- 解説
-

ん?大人と子どもがいる。
1人が1時間でする仕事量を1ってできない?
勝手に仕事量をおきたかったのに・・・
「大人1人が1時間でする仕事量」と「子ども1人が1時間でする仕事量」の比は、現段階ではわからないね。
でも、大人1人が1時間でする仕事量を、例えば1とおいて解き進めていけば、子どもが1人が1時間でする仕事量がいくらなのか計算することができるってわかるかな?
逆でもいいよ。子ども1人が1時間でする仕事量をたとえば1として解き進めていけば、大人1人が1時間でする仕事量がいくらなのか計算することができる。
もちろん、分数になる可能性も高いけどね。
では、子ども1人が1時間でする仕事量を1としてみますね。
すると、
子ども15人が1時間でする仕事量は15
子ども15人が4時間でする仕事量は60
全仕事量は60だと分かりました。つまり、大人6人が7時間で60の仕事をするから・・・
あ、これは分数になりますね。
大人1人が7時間でする仕事量は10
大人1人が1時間でする仕事量は\(\displaystyle \frac{10}{7}\)
上手に解けているよ。
このまま分数で計算を進めてもいいし、分母の7をはらってから解いてもいい。
分母をはらうのが圧倒的におススメだけどね!
分数は嫌だし、全体を7倍しますね。
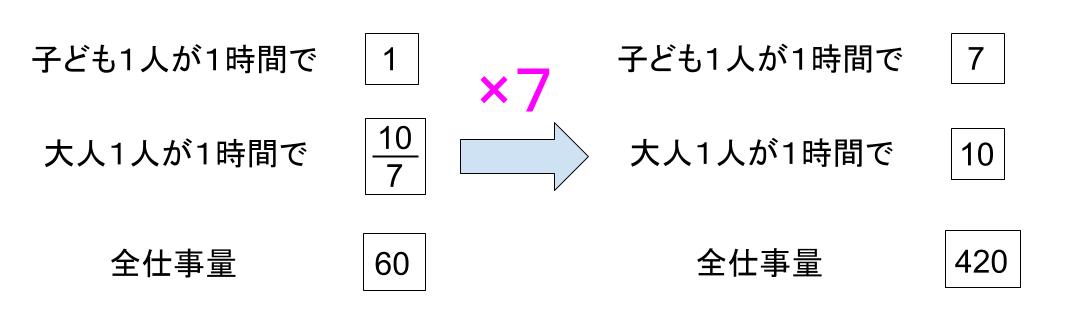

全仕事量は420
子ども1人が1時間でする仕事量が7
大人1人が1時間でする仕事量が10
続きはもう簡単ですね。
この仕事を大人7人、子ども2人ですると1時間の仕事量は、
10×7+7×2=84だから、420÷84=5
5時間で終わります!
はい正解です。とてもよくできました!

解けましたけど、先生・・・
はじめからうまい数を選ぶための、何かいい方法はありますか?
結局はじめにいくつとおけば計算が楽になるのかわからないから、途中でやり直しをしました。7倍のところです。
ないわけじゃないけど、学くんの解いたやり方で100点満点だよ。
途中で分数がでてきて、それで全体を何倍かする程度のやり直しなんて、面倒がっていてはいけないな。
はい。でも。
ないわけじゃないって・・・あるんですね。
うん、ある。
ではその解き方の例を見せるよ。
大人1人1時間で1
子ども1人1時間で①とする。大人6人1時間で6
大人6人7時間で42これが全仕事量同様に子どもで計算すれば、全仕事量は〇60
よって、全仕事量は、42であり、〇60だから、
42=〇60これは言いかえると
「ある仕事があって、大人が1人ですれば42時間かかり、子どもが1人ですれば60時間かかる」
ということですね。
あ!これって普通の仕事算だ。
42と60の最小公倍数は420、これを全仕事量とします。
あらためて全仕事量は〇420
1時間の大人の仕事量は⑩
1時間の子どもの仕事量は⑦とおけます。1時間の大人7人と子ども2人の仕事量は、
⑩×7+⑦×2=〇84
〇420÷〇84=5
5時間で仕事が終わります。
解けました。
はい。そういうことです。正解!
大人6人が7時間でする仕事は、大人1人が42時間した仕事と等しい。
このような見方を「のべ」といいます。
のべ?

うん。
「誰が」という見方をなしにして、総量だけに注目する見方だよ。
覚えておこうね。
