仕事をするグループと割合のパターン
- 例題3
- 大小2つの倉庫の整理を何人かで行います。大倉庫の仕事量は小倉庫の仕事量の2倍です。最初の2時間は全員で大倉庫の整理をしました。このあと半分ずつにわかれ、1時間整理をしたところ、大倉庫の整理は終わりましたが、小倉庫の整理は終わりませんでした。そこで、全員で残りの整理をしました。この仕事は、作業開始から全部で何時間何分かかって終わりましたか。
- 解説
-

これも具体値がいっさいないね。だから、勝手に数値を決めればいいのだけど・・・

全員で仕事をするか、半分で仕事をするか。
ここがポイントですね!「半分」は比の言葉です!全員が1分でする仕事量を2
半分が1分でする仕事量を1
とします!
おお!素晴らしいね。
ここさえクリアすれば、あとは整理して計算するだけで答えがでるよ。
最初の2時間=120分は全員で大倉庫の整理
2×120=240次に、半分に分かれて1時間=60分整理
1×60=60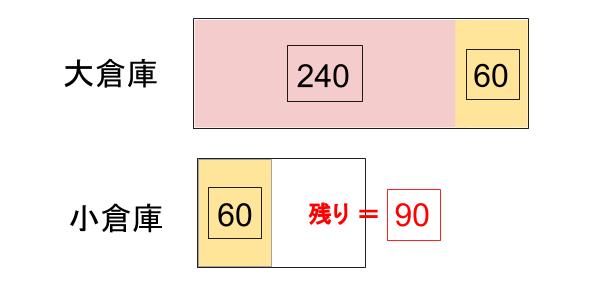

大倉庫はこれで整理が終わったのだから、
大倉庫の仕事量は240+60=300小倉庫は大倉庫の半分なのだから、150
つまり、小倉庫の残りの仕事は150-60=90
完璧ですね。あとちょっとで解けますね!

90を全員で整理する。
全員が1分でする仕事量を2としたのだから、
90÷2=45
求まりました。45分ですね。

答えは45分じゃないよ。
もう一回情報整理したものを見返してから答えてね。
あ!全員で2時間やって、半分で1時間やって、最後に全員で45分だから、合計は3時間45分です。

OK!大正解です。
完璧な解き方だったよ。ちなみに別解もあるよ。
大倉庫の仕事量は300
小倉庫は大倉庫の半分なのだから150
とわかったところで、
仕事の総量は450であることがわかる。
そして、整理する人は全員、休むことなく仕事をしている。
大倉庫の整理なのか小倉庫なのかはともかく、とにかく仕事をし続けている。
だから、
450÷2=225(分)225分=3時間45分
これでも正しく求められます。
ああ、なるほど。
