【和と差】消去算・その4

確かに、これはボクのやった差を何回もとる解法だと難しそうです。

先生の教えたやり方で練習してみようね。

まずはこうですね。

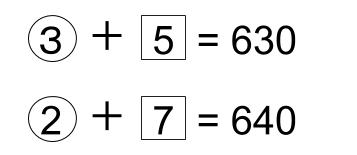
えーっと、どうするんでしたっけ。

式を何倍かすることで、黒（白）の数をそろえるんだよ。〇か□の数値をそろえるってことだよ。

「そろえると消せる」でしたね。
〇（黒）の方をそろえるなら、③÷②＝1.5倍　

あれ、②＋７＝640　
を1.5倍すると、
③＋10.5＝960　
　　　　
□（白）の方が、10.5になる・・・

先生っ！白玉が10個とあと「半分」になります。
白玉って割っていいんですか・・・？？

実際に白玉を割るわけじゃないからね。ダメな理由はないでしょう。

・・・なんか混乱してます。助けてください。

小数や分数が苦手な子はとても多いのだけれど・・・これに関してはたくさん経験して慣れるしかない。　　

ところで・・・・小数が嫌なら整数だけで解決しよう。

③と②を、最小公倍数の⑥にそろえると計算がやりやすいよ。おススメだ。

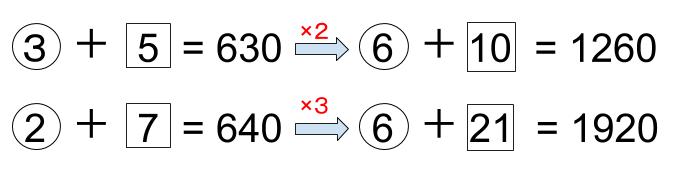
ああ、なるほど。2つの式を書き直すんですね。

残りは今までとまったく同じだから大丈夫だよね？

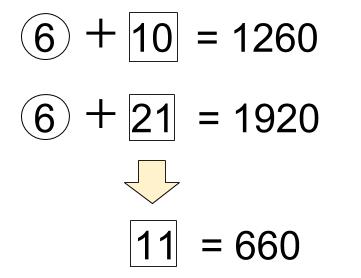
⑥＋10＝1260
⑥＋21＝1920

差をとれば、

11＝660　　　
11で割って、　　　
１＝60

あとはこれを使って、どの式でもいい。①が求まるよね。

③＋５＝630
を使えば、

③＋60×５＝630
③＝330
①＝110

１＝60
だから、白は１個60ｇ
①＝110
だから、黒は１個110ｇ
ということですね。

うん、そういうことです。

ところで、この問題だけど、「白玉をそろえて消す」方法で解いてみて。

白は５と７だから、最小公倍数の35にそろえますね。

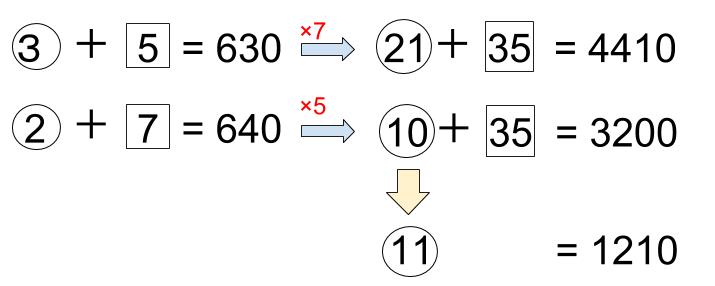
差をとると、⑪＝1210、
1210÷11＝110より、
①＝110
あ、さっきと同じ答えだ。求まりました。黒玉1個110ｇです。

お見事！ところで、白をそろえて消すと、まずは黒が求まるよね。
はじめは黒をそろえて消して、白から求めた。

だから、「求める方と逆をそろえて消そう！」ということが解法テクニックのように指導されている、いろんな塾で。

でも先生はこの視点はそんなに大事じゃないと思っている。

その理由は？

黒を求めたら、いきなり答えを書くんじゃなくて、さっと確かめをすべきだから。
白も求めて、矛盾が起きていないことの確認をする。たいした時間かからないからね。

それにね、さっき白を 35にそろえて解いたよね。
ちょっと計算が面倒だったでしょ？
式を７倍するのとか。

あ、はい。ちょっとだけですけど。　
黒をそろえたときは、２倍と３倍だったから楽だったです。

ということです。
１．そろえるための計算が楽な方を選ぶ。
２．片方が求まったら、もう片方も求めて確かめをするべき。
この姿勢が正解です。

あとね。学くんがはじめにやった1.5倍なんだけどね。
あれだって素晴らしい解き方だよ。

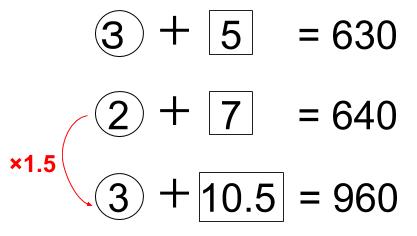
差をとって、5.5＝330
　　
330÷5.5＝60が暗算で出せるくらいが良いのだけど、　　　

5.5＝330　
は２倍すれば、
11＝660
さすがにこれは、１＝60
を暗算できるよね！！

もちろん残りの計算を今までと同じようにして、①＝110を求めればいいね。