過不足算
「差集め算」なのか「過不足算」なのか、名称にこだわる必要はありません。
大手進学塾で4年生後半くらいで教えられている内容です。やや難しいため、真の理解に至らないまま、その場しのぎの解法暗記で乗り切る子どもを量産しています。もちろん久しぶりに実力テストで出題されるとできません。
ただし、過不足算ができなくとも、致命傷にはなりません。過不足算が出題されたときに点がとれないだけで済みます(消去算ができないと致命傷になります。今後あらゆる所で使うからです)。また、4年時に習う”差集め”の解法が難しくてどうしてもダメだった生徒が、比を用いた別解だとすんなり理解できたりします。
あるいは6年生になってから、差集めを理解できるようになる子もいます。
どうしても理解できないときは、速さや割合など、他の重要単元の学習をしましょう。
いつかまた戻って学びなおしてくださればオーケーな単元です。
過不足算の指導方法はかなりたくさんあります。
当テキストの解説が究極決定版であると自信をもっておすすめいたします。
注 もちろん、多様な別解を否定するつもりはありません。別解とあわせて、より深い構造の理解につながっていくのが真実だからです。
あまりとぴったり
例題1
生徒たちに折り紙を配ります。4枚ずつ配ると24枚あまり、6枚ずつ配るとちょうど配れます。折り紙は全部で何枚ありますか。
解説

今日はこんな問題からスタートだよ。

この問題は、以前にやった問題と似ている気がします。
まず4枚ずつ配って、手元には24枚残っている。
この24枚を、1人に2枚ずつ追加で配ったんだから・・・
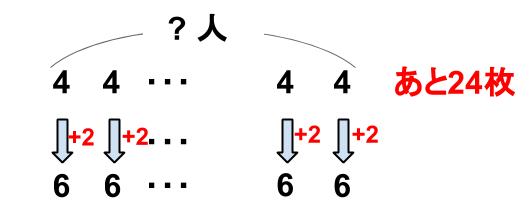

24枚がちょうど配れた。
つまり、24÷2=12
12人います。
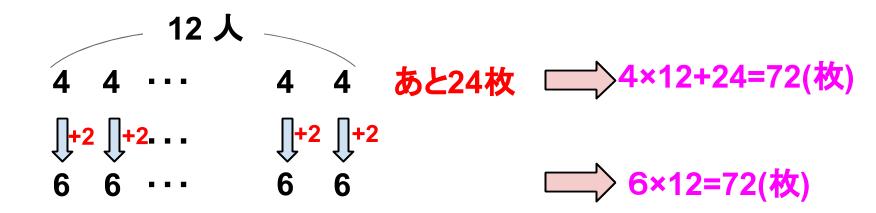
だから、折り紙の枚数は、6×12=72(枚)です。

うん、正解です。
今までの学習がきちんと身についているようだね!素晴らしいよ。
もう一つの条件でも同じ枚数になることが確かめられるよね。
4枚ずつ12人に配って、さらに24枚
4×12+24=72
矛盾がおきないんだから、これで絶対に正解だね。
文章題はこのような確かめができる。
自分の答えが文章題の条件すべてにうまくいっているかどうか、確かめるクセをつけましょう。
