差集め
個数を逆にする
例題1
1個80円のりんごを5個と、1個50円のみかんを2個買うつもりでしたが、りんごとみかんの数を逆に買ってしまいました。予定の金額よりいくら高くなりましたか、あるいはいくら安くなりましたか。
解説

計算問題ですよね
80×5+50×2=500・・・予定
80×2+50×5=410・・・実際
500-410=90
90円安くなりました。

うん、正解だよ。
学くんのように計算をしても答えはでますが、
「差とは何なのか」を考察したくてこの例題を出しました。
これは具体図で表せる状況だよね。


予定と実際で差を取ります。
このとき、等しいところ以外で差をとればよいですね。
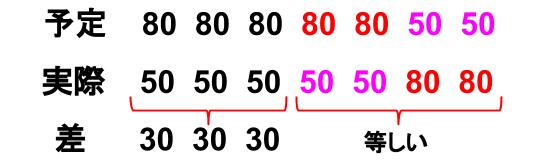

80円3つを、50円3つにかえたら、
30×3=90
90円安くなった!

へえ。なるほどね。

差をとるというのは、
どこからどこまでが同じかを見極めて、同じ部分は無視すること
とも言えるんだよ。
で、この問題は面積図との相性が良いです。
問題文もつるかめ算みたいでしょ。
2つの異なるものを、何個かずつ買ってるわけだし。


そして、この2つの面積の差は、下図のように表せるね。
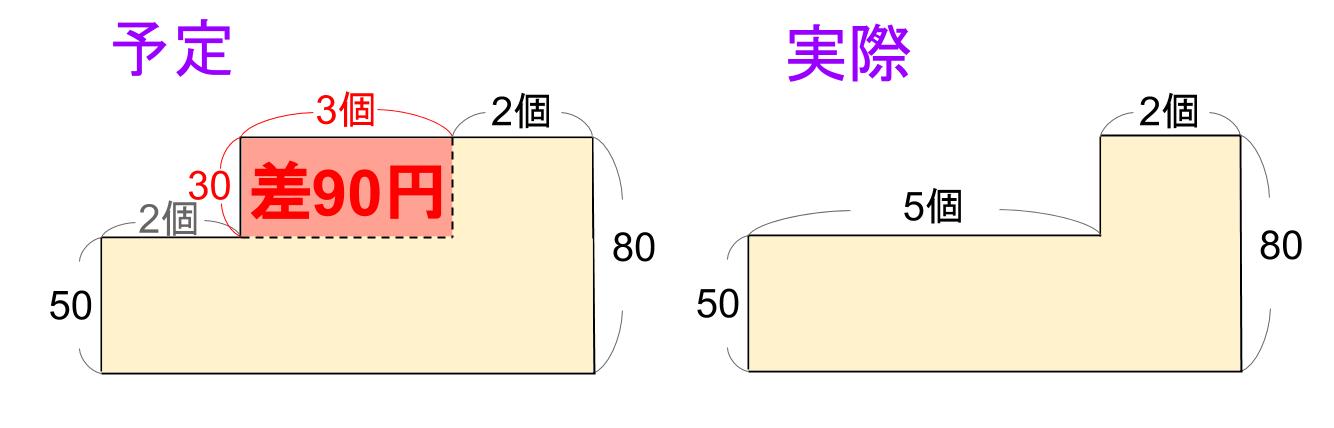

なるほど。
すっきりと見やすい図ですね!
例題
りんごを6個と、みかんを4個買うつもりでしたが、りんごとみかんの数を逆に買ってしまいました。りんご1個はみかん1個より60円高いです。予定の金額よりいくら高くなりましたか、あるいはいくら安くなりましたか。
解説

じっさいいくらだったのか、計算できないですね。

さっき先生が書いたように、面積図にしてみてごらん。

えっと・・・予定と実際とどっちが高いんだ?

どっちが予定で、どっちが実際なのかは後で考えてもいいよ。
まずは、2つの面積図を用意してしまおう。
その図をみながら、どっちが予定でどっちが実際なのかを考えてもOKだ。
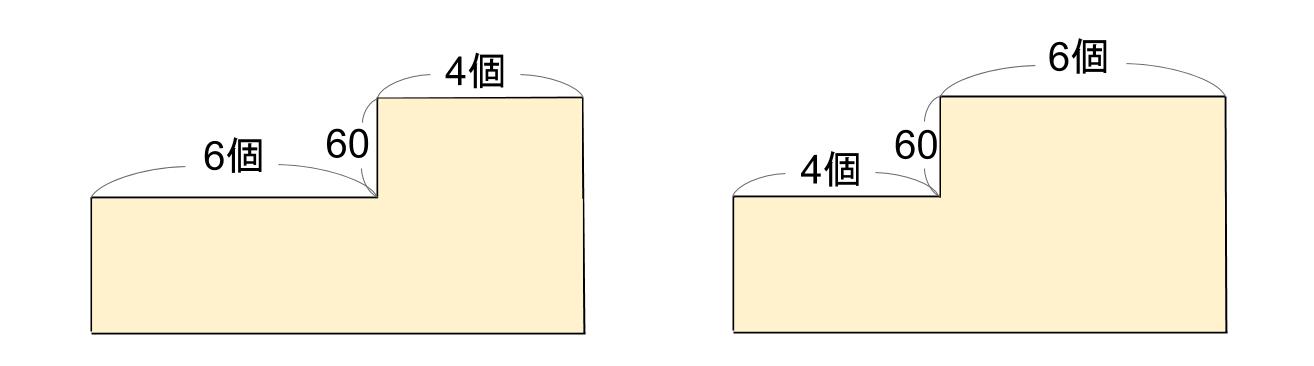

りんごのほうがみかんより60円高い。
高いりんごを6個買ってる方が「予定」だ。
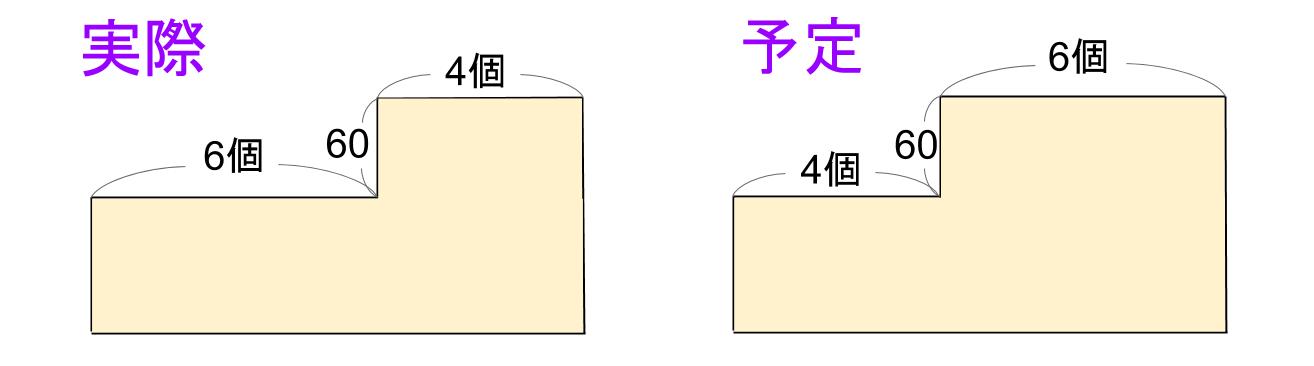

2つの面積の差は下図のようになります。
りんごはみかんより1個60円高いから、60×2=120
差は120円
つまり、実際は120円安くなります。
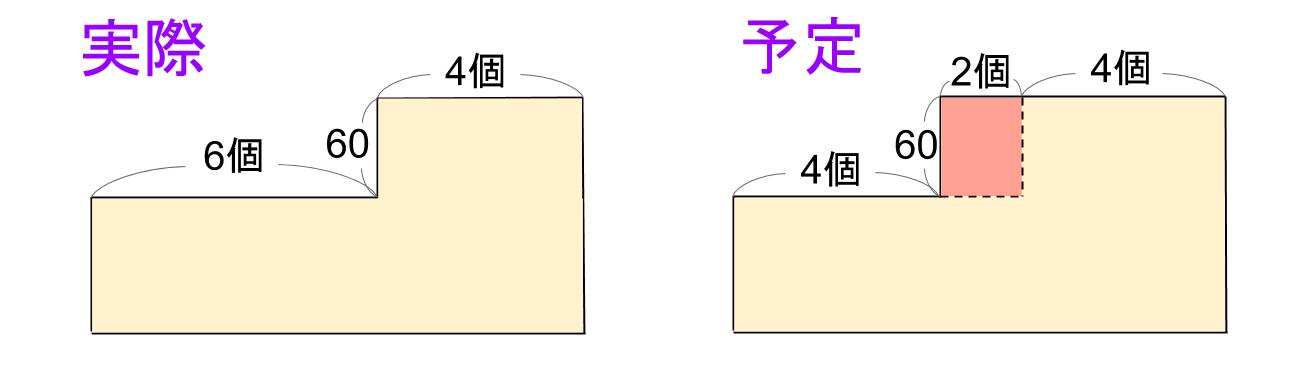

とても上手に図がかけたね。
正解です。
