【割合】全体に対する割合・その1

さて、割合の基礎学習もこれで最後の単元だ。

いよいよ割合マスターですね！

マスターにはまだなれないけど、基礎はすべて終了だ。
基礎ほど大事なものはないからね。
　　　　　
さて割合は、ＡはＢのＰ倍、という見方だと教えてきたんだけど、その中でも特に、
全体から見て、その部分は何倍か、という見方がよく使われるんだよ。　　

何のことだかわからないです。

そうだね、さっそく具体例で見ていこう。

なんなの、この変な問題。
もちろん、女子が多いのは吹奏楽部です。
36人と24人では、36人の方が多いに決まってます。

そうだね。もちろん正解だ。
しかし、「女子が多い部活」とは別の意味もあるでしょ。
「女子だらけで、男子が少ない部活」という意味だ。
２つの部を下の表のようにまとめてみる。　　　

　　　　　　　　　
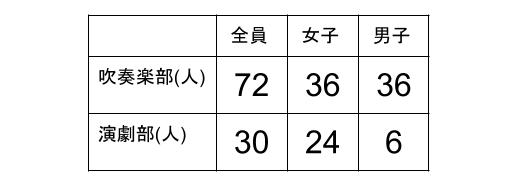
吹奏楽部は男子と女子が同数だ。
一方、演劇部は女子だらけの部活であることが分かる。
男子はあまりいない部だ。

それぞれの部活が、どれくらい女子だらけなのか（女子があまりいないのか）をきちんと数値で明らかにしたい。
ここで割合が大活躍するんだよ。

割合は２つのものが何倍なのかってことですよね？

そうだね。今回は、「全人数の何倍が女子なのか」という視点なんだ。　
吹奏楽部はどうかな？女子と全体を比べると・・・？

吹奏楽部は全部で72人いて、その半分が女子です。

その通り！！

「半分」というのは、そもそも全体との比較を考えている言葉だよね！

全体の0.5倍（\(\displaystyle \frac{1}{2}倍\))の量を半分という。この言葉を知ったのはいつかな？

このときからすでに割合の学習をしていたってことなんだよ。

　　　
「半分」は、幼稚園くらいから知ってるかもね。

「半分」のように、全体に対して何倍だろうか、という考え方は日常的によくする考え方だよ。
　　
さて、この見方で２つの部をまとめてみるよ。下図のようになるね。

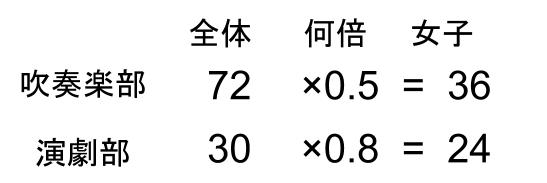
この「～倍」を、「全体に対する女子の割合」といいます。
この聞きなれない言い回しをしっかりと覚えようね。

吹奏楽部全体に対する女子の割合が0.5である
演劇部全体に対する女子の割合が0.8である　　　　　
このように言います。

なんだかずい分堅苦しい言い方だな。

そうだね。あまりこの言い方は出てこないんだけれど、
出てきたときに意味が分からないでは困ってしまうから、
わかっておこうね。

さて、どれくらい女子だらけの部活なのかは、割合を見ればわかります。
割合の数値が大きいほうが女子だらけだよ。
もちろん演劇部のほうが女子だらけの部活です。
０．５と０．８では、０．８の方が大きいですからね。

割合の数値が0.5だと、半分なんだね。

とても良い視点だね。

ところで、もっとも女子だらけな部活ってどんな部活かな。

バトン部です！！全員女子です。　

男子がバトンをやってるケースもあるんだけどね。男子新体操とか知ってる？知らなくてもいいか。
全員女子というのが、一番女子だらけな部活だね。
逆にもっとも女子が少ない部活は？

男子ラグビー部です！

そうだね、ラグビーやってる女子もいるだろうからね。
でも男子ラグビー部なら、男子しかいない部だね。

全員が女子のとき、その割合は1だ。
「全体」に対して「全体」の割合は1、
全体×1＝全体　
ですからね。

以下のような言い方になる。
バトン部全体の１倍が女子である
バトン部全体の100％が女子である
バトン部全体の10割が女子である

逆に、まったくいないとき、その割合は0だね。

割合は０から１の間になるんだ。

でも、「今日の入場者数は昨日の入場者数の1.25」
っていうのを前の回で見たよ。
これは割合が1をこえてるよね？

うん。それはそれでいいんだ。割合が1.25になって何の問題もないよ。
今日の話題は、「全体に対する部分の割合」の話だよ。
この考え方のときは、割合が0から1の間になるよ。
全体から見て、その部分がどれくらいなのか、ということだからね。