相当算・基礎
直接相当
例題1
全体の人数の \(\displaystyle \frac{3}{4}\) が男子であり、男子は全部で48人います。
全体の人数は何人ですか。
解説

えっと・・・新しい内容ではないですね。
(全体)× \(\displaystyle \frac{3}{4}\) =48
全体は何人なのか求める。

その通り。
新しい問題ではないので、とにかく答えをだしてください。

(全体)× \(\displaystyle \frac{3}{4}\) =48
左右を4倍すれば、
(全体)×3=48×4
左右を3で割れば、
(全体)= \(\displaystyle \frac{48×4}{3}\) =64
全体は64人です。

はい、正解です。
かけ算の逆算なので、48÷\(\displaystyle \frac{3}{4}\) で求めてもよいし。
まあ、きちんと素早く正解できれば良いのです。
ところで。
このような問題は、頭の中で図としてイメージできるようになっておくと強い。
下図のようになっています。


なるほど!
48÷3=16
1山が16人ですね。
全体は4山だから、
16×4=64
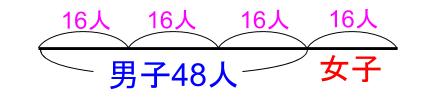

そういうことです。
図で考えると何を計算しているのかが明確になるよね。
ところで、
「1山が16人」だったのだけど、
「1山が16人に相当する」とも言います。
それで、このタイプの問題を「相当算」と言います。
これも「~算」という名前にこだわる必要はまったくないですけれど。
