例題1・再掲
下の□にあてはまる数をそれぞれ答えなさい。
(1) 30は240の□倍です。
(2) □は60の \(\displaystyle \frac{4}{5}\) 倍です。
(3) 120は□の0.75倍です。
解説

では、答えあわせからだよ。
答えは
(1)\(\displaystyle \frac{1}{8}\) または0.125
(2)48
(3)160
何問できたかな?

・・・1問です。時間が短すぎます・・・

ぜんぜん楽勝でもなかったね。
大丈夫。多分そうだろうと予想していたからさ。
苦手な子は、以下の2タイプのどちらかだ。
こういう子をたくさんたくさん見てきたよ。
1、そもそも分数の計算が苦手な子。
まずは、とにかく練習して素早く計算できるようになることが大事。
当たり前だけど、この反復練習をやらないで次に進むことはできないよ。
九九がスラスラ言えない状態で、次に進めないって想像できるよね。
分数の計算も同じ。スラスラ楽勝でできるというのが大事だ。
2、分数の計算はたくさん練習したし得意だけれど、さっきの例題のように文章で出題されると苦手な子。
このタイプも非常に多いですね。
文章での計算練習をあまり多くやってこなかったからだろうね。

確かにこういう問題はほとんどやったことがないな。

入試問題は、このような文章をさらに複雑に組み合わせた問題が出題される。
立ち向かうためには、もっとも単純なこの例題がスラスラ解けるようになることからはじめるしかない。基礎固めは最重要課題だからね。
順番に解説していこう。
(1) 30は240の□倍です。

時間が短いとあせります。普段ならミスらないのに、
240÷30=8
としてしまいました。

正しくは、30÷240 をすることで求められるわけだけど、
30÷240なのか240÷30なのか迷ってしまう・・・
という人は多いね。
よく練習して、確実に素早くわかるようになろうね。
では、このような問題を確実に素早く処理する手順を教えるからね。
まず問題文をそのまま算数の式に書き換えます。
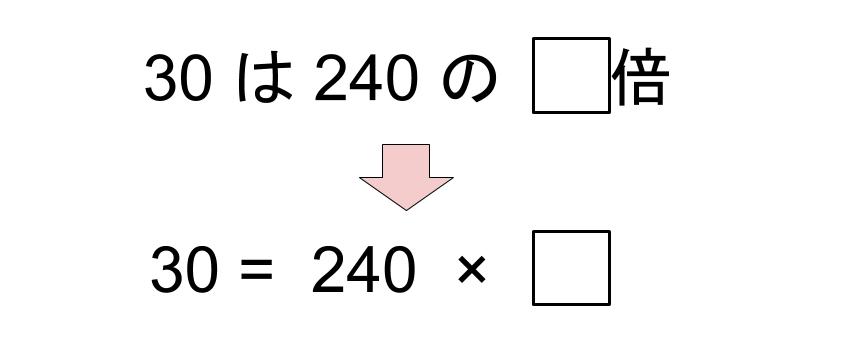

あとは、この□を正しく計算できればOKですね。
この□に入る値の計算方法で迷いますか?
迷わないでくださいね。
計算なんてまったくいらないのですから!
30と240を上下に並べて、分数にするだけなのですから。
\(30=240×\displaystyle \frac{30}{240}\)
です。
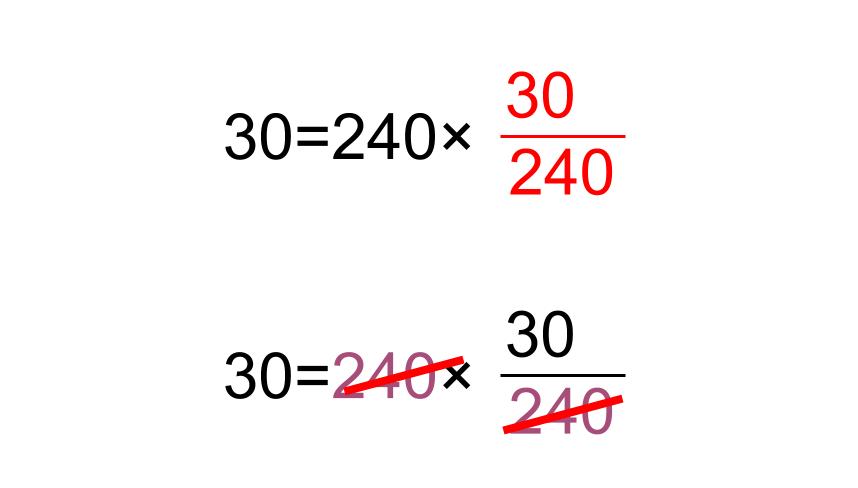

一切計算をする必要がないんです。
ほんの1秒くらい \(\displaystyle \frac{240}{30}\) と \(\displaystyle \frac{30}{240}\) のどっちかな?
と頭の中で迷ってもいいですけども。
どちらを分子にするか、ただの2拓です。
これが分数の威力です。
もちろん約分の必要があるときは約分します。
\(\displaystyle \frac{30}{240}= \displaystyle \frac{1}{8}\)
以上求まりました。

なるほど・・・
計算問題を解いたって感じがしませんね。簡単すぎて。

簡単でうれしいでしょ。
分数を使わないならば、
30÷240=0.125
という下のような筆算をしなくてはならない。
ちょっとめんどうだよね。
このような計算を一切しないで済ませてしまうのが分数なんです。
分数の力は絶大ですよ。
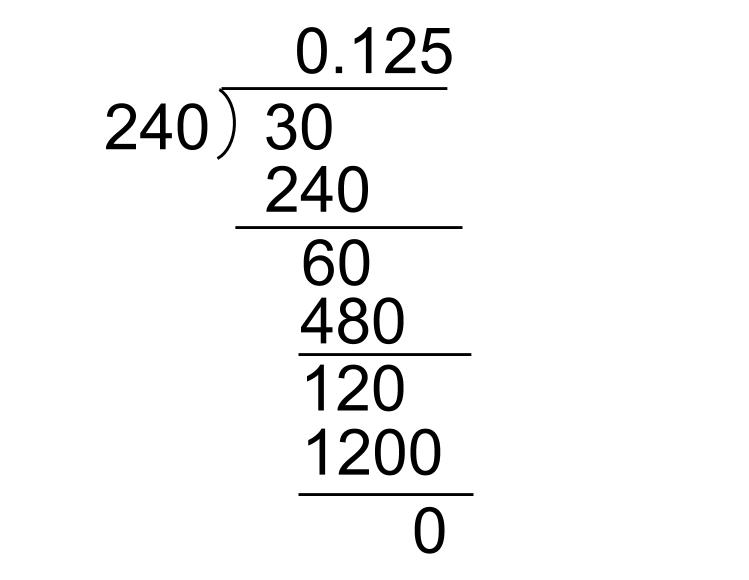

なるほど・・・でも約分があるんですね。

約分をめんどうがっていてはいけないよ。
約分のおかげで、ケタ数の多い筆算をしなくて済むんですからね。
ケタ数の多い筆算の計算練習をするのではなくて、約分が苦も無くスラスラできるようになるための練習をした方が絶対に有用です。
そのためには、公約数を苦もなく見つけること。
÷2、÷3、÷5などの簡単な計算は暗算でだせること。
このような練習をして、約分がスラスラできるようになることが、算数が得意になるためには絶対に必要なんだよ。
それに「約分」は、中学、高校に行っても必須の重要能力だからね。

はい、約分、がんばります。

あとね、分数で処理すべき理由はもう1つあるんだ。
わかるかな?

えっと・・・わかりません。

分数でやるべき理由
それは、
「割り算は、割り切れないことがあるから」です。
今回は、30 ÷240=0.125 と割り切れたけどね。
分数を使わないと無理、という問題だってありますからね!
例えば、5は7の何倍か求めたいとき。

なるほど。
5÷7=0.714285・・・
これは永久に割り切れない計算ですね。
だから、5は7の \(\displaystyle \frac{5}{7}\) 倍
と分数を使う。

正解!
そういうことです。
