【割合】導入・その3

この１問だけ正解でした。

今回の３題のうち、最も簡単な問題が（２）だね。
３題すべて、かけ算を文章にして出題しているだけですが、
（２）だけが、そのままかけ算をすれば答えがでます。
他の２題は逆算になりますからね。　

問題文をそのまま算数の式に書きかえてみると・・・

□はそのまま計算をするだけで求まりますね。　　　　
答えは48です。　

時間がなくて最後まで計算できませんでした　　

120÷0.75を筆算してたのかな？
やはりこの問題も、分数を活用することで面倒な筆算を減らしたいね。
　　　
では１つ１つていねいに解説していくよ。

まずは、そもそも□の求めかたで迷ってしまう人へ！
問題文をそのまま算数の式に書きかえるのです！

あとは逆算をするだけですね。

どう？迷わずできるかな？

小数とか分数だと不安かも・・・
□＝120÷0.75 なのか、□＝120×0.75なのか・・・・
迷っちゃいますね。

では、いろいろな計算処理方法を教えていくぞ。

まずは、分数の約分の利用だ。
120と0.75を上下に並べるだけ！

□= \(\displaystyle \frac{120}{0.75}\) であることがわかります。

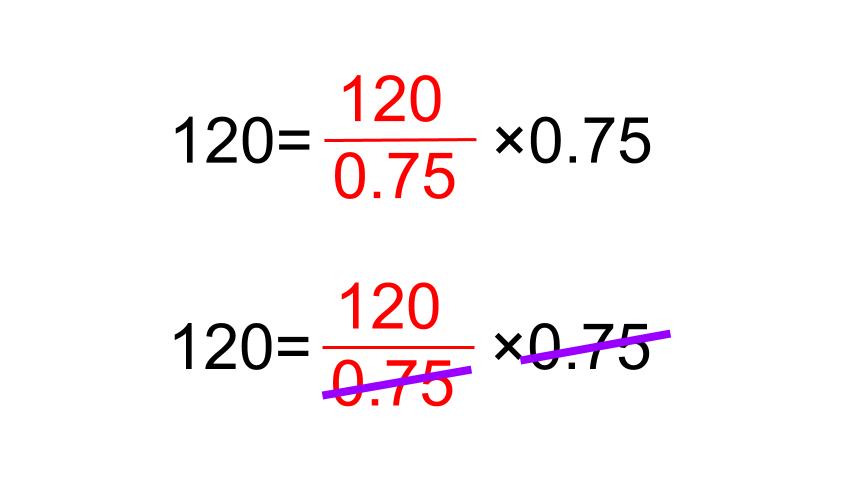
え？なにこれ・・・ \(\displaystyle \frac{120}{0.75}\) ！？
こんなのありですか？

ありだよ。
とにかく見慣れてくださいな。

\(\displaystyle \frac{1}{2}=\displaystyle \frac{3}{6}=\displaystyle \frac{30}{60}\)

のように、

\(\displaystyle \frac{120}{0.75}\) の分子と分母に同じ数をかければ、見慣れた分数になる。

じゃあ、分子と分母を100倍して、

\(\displaystyle \frac{120}{0.75}=\displaystyle \frac{12000}{75}\)

あってるよ。あとはどんどん約分をしていけばいい。

\(\displaystyle \frac{12000}{75}=\displaystyle \frac{2400}{15}=\displaystyle \frac{480}{3}=160\)
　
求まりました。160です。

正解！
ところでね、

\(\displaystyle \frac{120}{0.75}=\displaystyle \frac{12000}{75}\) としたところだけど、

分子と分母に２をかけていくと、　　　　

\(\displaystyle \frac{120}{0.75}=\displaystyle \frac{240}{1.5}=\displaystyle \frac{480}{3}\)

どう？

あ！計算が楽ですね。
480÷３＝160　　
簡単だ！

やみくもに10倍、100倍するのではなくて、もっと簡単な計算がないかアンテナをはっておこうね。