線分図を積極的に利用したいパターン
- 例題2
- 3人でおはじきを分けます。Aは全体の \(\displaystyle \frac{1}{3}\) より4個多くとりました。Bは残りの \(\displaystyle \frac{3}{5}\) をもらいました。最後に残った12個をCがとりました。はじめにおはじきは何個ありましたか。
- 解説
-

さっきと同じように、線分図にしてみますね。
Aは全体の \(\displaystyle \frac{1}{3}\) より4個多くとりました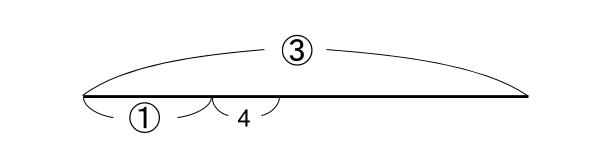

うん、とてもいい図だね。

残りの \(\displaystyle \frac{3}{5}\) がB、 \(\displaystyle \frac{2}{5}\) がC
そのCが12個
下図のようになりますね。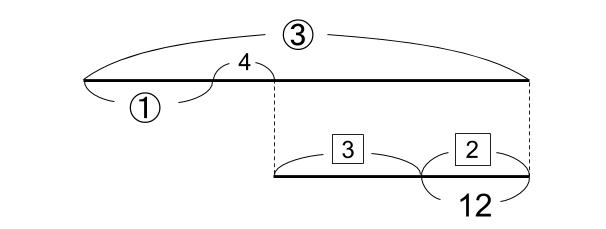

2=12だから、
5=30
で次は・・・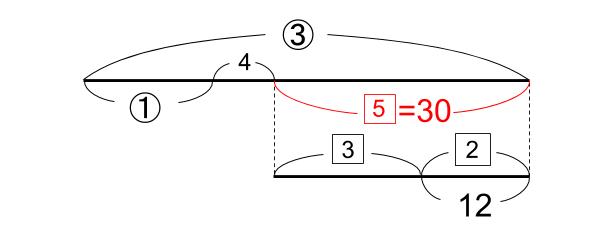

□の世界は解き明かしたのだから、次は、③とか①との関係を見ればいいね。

あ!②=34ってことだ!
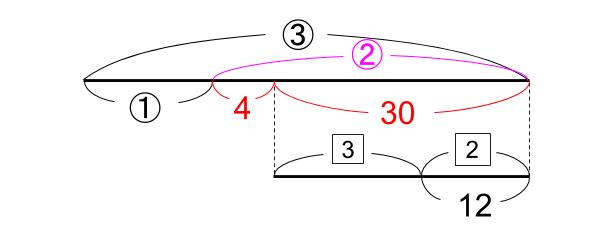

②=34ならば、①=17
つまり、③=51
はじめのおはじきは51個です!
大正解!素晴らしいね。
保護者さまへ
線分図がもっともおススメなのですが、もし式だけ解くと下のようになります。
{①-(〇\(\displaystyle \frac{1}{3}\)+4)}×\(\displaystyle \frac{2}{5}\)=12
このような式を解くのは、小学生にはおススメできません。
