2段階、3段階に割合を考える
- 例題1
- 上から落とすと、いつも同じ割合ではね上がるボールがあります。3mの高さから落としたとき、1m20cmの高さまではね上がりました。このボールをある高さから落としたところ、3回目にはね上がった高さが16cmになりました。はじめ何cmの高さから落としましたか。
- 解説
-

こんな図を想定できた?
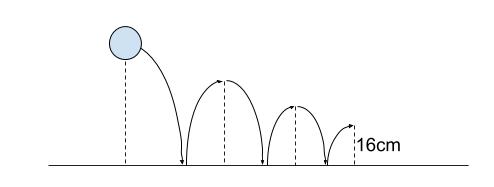

はい!
300cmから落として、120cmはねあがる。これはつまり、落とした高さの、\(\displaystyle \frac{120}{300}=\displaystyle \frac{2}{5}\) まではねあがるということ。
この \(\displaystyle \frac{2}{5}\) 倍という分数のかけ算が連続してるってことですね。

その通り。

□\(×\displaystyle \frac{2}{5}×\displaystyle \frac{2}{5}×\displaystyle \frac{2}{5}=\)16
つまり、□=16×\(\displaystyle \frac{5}{2}×\displaystyle \frac{5}{2}×\displaystyle \frac{5}{2}\)=250
答えは250cmです。
うん、正解です。
ところで連比でも解けるでしょ。

あー!言われてみればそうですね。

うん、でも連比で解く方が面倒じゃないかな?
分数のかけ算のほうが有効なときもある。
前の単元でも言ったのだけれど、どちらでもできることが理想だよ。
問題によって、より楽な方を選べれば最高だよ。どちらも同じ解き方で、見た目が違うだけなのです。
- 例題2
- A球,B球を真下に落とすと,A球は落ちた高さの \(\displaystyle \frac{3}{4}\) ,B球は \(\displaystyle \frac{2}{3}\) の高さまではね返ります。A球,B球を同じ高さから真下に落としたら,2回目にはね返った高さの差が34cmでした。はじめに落とした高さは□cmです。
- 解説
-

分数のかけ算で表せそうです。
(Aはじめ)\(×\displaystyle \frac{3}{4}×\displaystyle \frac{3}{4}\)=(A2回目)
(Bはじめ)\(×\displaystyle \frac{2}{3}×\displaystyle \frac{2}{3}\)=(B2回目)
となります。
で・・・次は・・・わかりません。
かけ算の式は、「比」が与えられたのと同じことだよ。
(Aはじめ)\(×\displaystyle \frac{3}{4}×\displaystyle \frac{3}{4}\)=(A2回目)
なんだから、
(Aはじめ)\(×\displaystyle \frac{9}{16}\)=(A2回目)
つまり・・

Aはじめが⑯で、A2回目が⑨です。
なるほど。
じゃあ、
(Bはじめ)\(×\displaystyle \frac{2}{3}×\displaystyle \frac{2}{3}\)=(B2回目)
より、
(Bはじめ)\(×\displaystyle \frac{4}{9}\)=(B2回目)Bはじめが9で、B2回目が4だ。

そうだよ。
で、A、Bは同じ高さから落としたのだから・・・
Aのはじめ⑯=Bのはじめ9
異なる2つの比がつながった!
連比をします。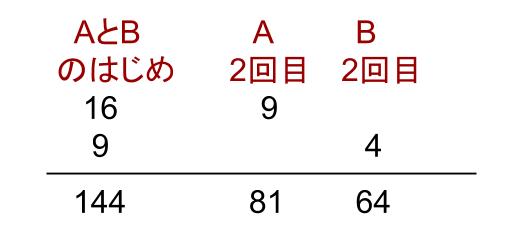

改めて、
AとBのはじめ=144
A2回目=81
B2回目=64
とすると、
A2回目とB2回目の高さの差は、
81-64=17
つまり、
17=34cm
17で割って、
1=2cmだ。はじめに落とした高さは、144=288cm
求まりました。288cmです!

正解だよ!
さらに理解を深めるために、異なる道筋の解き方も見ておこう。
まず、
(Aはじめ)\(×\displaystyle \frac{3}{4}×\displaystyle \frac{3}{4}\)=(A2回目)
から、Aはじめが⑯で、A2回目が⑨とおけた。次に、
(Bはじめ)\(×\displaystyle \frac{2}{3}×\displaystyle \frac{2}{3}\)=(B2回目)
なのだけれど、
Aはじめ=Bはじめ=⑯なのだから、⑯\(×\displaystyle \frac{2}{3}×\displaystyle \frac{2}{3}\)=(B2回目)
これを計算すれば、(B2回目)=〇\(\displaystyle \frac{64}{9}\) となる。
A2回目の⑨と、B2回目の〇\(\displaystyle \frac{64}{9}\) の差が、34cmなのだから、
⑨-〇\(\displaystyle \frac{64}{9}\)=〇\(\displaystyle \frac{17}{9}\)
より、
〇\(\displaystyle \frac{17}{9}\)=34cm17で割って、
〇\(\displaystyle \frac{1}{9}\)=2cm
9倍して、
①=18cm
とわかる。はじめの高さは⑯なので、⑯=18×16=288cm
求まりました。
なるほど。

このような割合・比の問題は、どこでもいいから①とか⑤とか、勝手においてしまえばいいのです。
もちろん1でもいい。記号は〇でも□でも△でもいい。そうすれば、あとは自動的に計算が進みます。
計算が楽になるような数値を決めて、計算をスタートするのがいいのだけれど、別にどんな値で計算をはじめても問題は解けます。
なぜなら、比は変わらないからです。

なんのことか、よくわからないです・・・

今回は、
(Aはじめ)\(×\displaystyle \frac{9}{16}\)=(A2回目)
(Bはじめ)\(×\displaystyle \frac{4}{9}\)=(B2回目)ということだった。
分からない値は、
(ア)(Aはじめ)=(Bはじめ)
(イ)(A2回目)
(ウ)(B2回目)
の3つ。どれでもいいから、勝手に数値を①とか⑤とか、なんでもいいから決めてしまえば、残り2つは自動的に決まるよね。
そして、その3つの比は絶対に一定だ。はじめにおいた数値とは無関係で決まる。
でも、もちろん、できるだけ計算が楽になるようにスタートした方がいいわけですね。
今回は、分母が16と9だから、どちらも約分できる数をはじめの高さとすれば計算が楽になりそうですね。
16と9の最小公倍数、144としたら楽そうです。
Aはじめ144\(×\displaystyle \frac{9}{16}\)=(A2回目)81
Bはじめ144\(×\displaystyle \frac{4}{9}\)=(B2回目)64
高さの差は17=34cm
より、1=2cmだ!
うん、連比で解いたときと同じ値になったね。
はじめの高さを144という計算が楽になる値にしなくとも、この問題は解ける。
この「問題の仕組み」を理解することが大事だよ。
