2つの異なる比をそろえる方法
- 例題1
- AとBの所持金の比は4:5、BとCの所持金の比は3:4のとき、AとBとCの所持金の比を求めなさい。
- 解説
-

AとBの所持金の比は4:5だから、
Aを④、Bを⑤とします。で次は、BとCの所持金の比は3:4だから、
Bを③、Cを④として・・・
あれ、先生!!
Bは⑤なのか③なのか、おかしなことになりました!
おかしいのは学くんの解き方がおかしいからだよ。
⑤っていうのは線分図を5山に分けたっていう意味だったよね。
Bを3つにわけるならば、その1つ分は①じゃだめだよね。こういうときは、
①とはちがう1山だという意味を込めて、1 とする。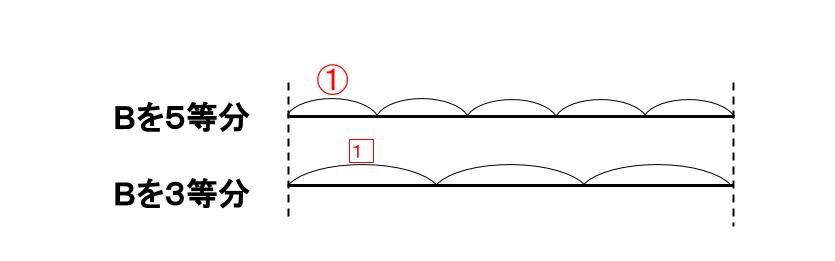

じゃあ、A=④で、B=⑤=3で、C=4ということか。
どうすればいいのかな?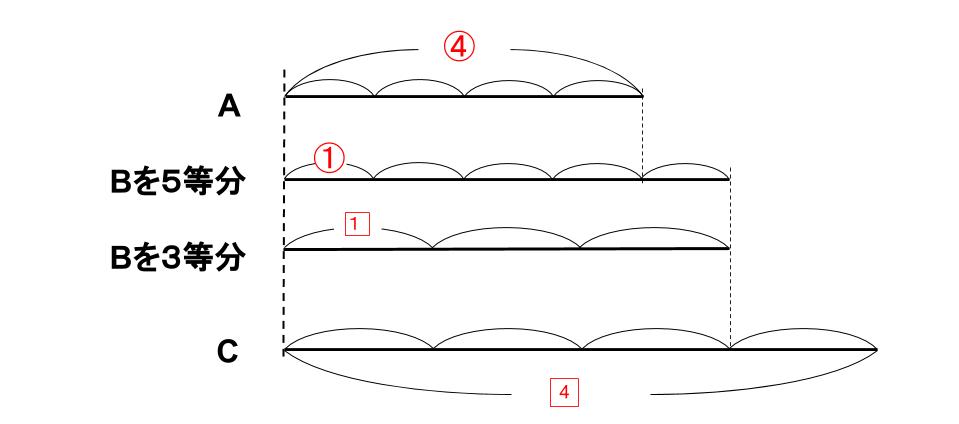

ポイントは、「Bを5等分するのか、3等分するのか、どっちにするのか」というところだ。コツを教えるよ。
ずばり、「5等分にも3等分にも対応できる、15等分とする」改めて、B=⑮としてみよう。
⑮の5等分は③、⑮の3等分は⑤だ。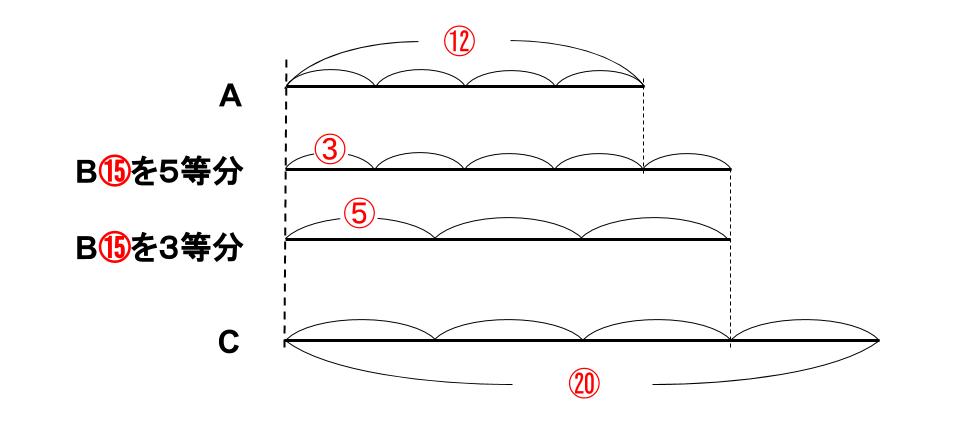

なるほど、A:B:C=12:15:20だ。

うん、それで正解だよ。

ところで。
上の解法と実質同じ解き方を、すっきりと表示する方法があるんだ。そもそも⑤とか⑮とかは、線分図を5等分、あるいは15等分したときの1山を表している。
それさえわかっていれば、線分図を15等分した図をかかなくてもOKだったわけだ。
以前にも学習したことだけど、とても便利な表記だよね。それをふまえて、線分図なしですっきりと解いてしまおう。
AとBの比は4:5、
BとCの比は3:4
これを下のようにかきます。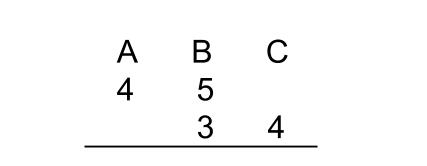

Bは5なのか3なのか。
結局どちらでもないっていうことを再確認してね。
Bという線分図を何山に分けようと自由だからね。このように、2種類の比のどちらにも登場しているのがB、
この共通部分Bを、2つの比の最小公倍数にするのがコツ。
今回の例なら15にしてみよう。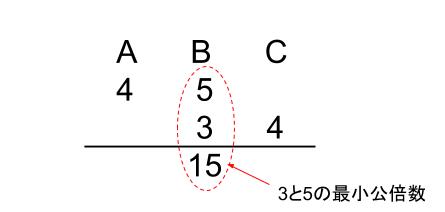

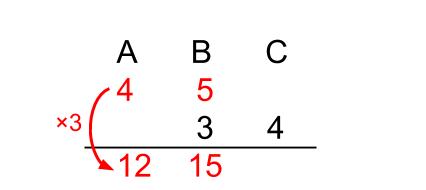
AとBの比は4:5=12:15だ。

BとCの比は3:4=15:20
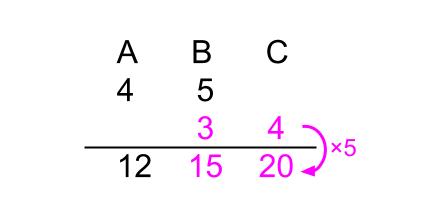

これで、求まったね。
A:B:C=12:15:20だ。
この解法を「連比」と呼んでいる先生もとても多いよ。
連比とは3つ以上を並べる比のことだけど、今回のように最小公倍数でそろえるこの解法を「連比」と呼んでいることが多い。今後、先生もこれを「連比」と呼ぶことにするよ。
ポイントをくりかえすと、
2種類の比は共通部分を最小公倍数にして、まとめて連比にできる!
なるほど。スッキリ解けますね。

うん。このまとめ方はとても便利だから、しっかり使いこなせるようになろうね。線分図で解いたときと「考え方はまったく同じ解き方」なんだけど、表記がすっきりと便利になった解き方だよ。

さらにもう1つの解き方を確認しておきたい。
「比・割合」というのは、結局は「~倍」を表しているにすぎないのだったよね。
これは最重要ポイントなんだけど、覚えているよね。
あ、はい。そうでしたね。

だから、かけ算をするだけでこの問題は解ける。
AとBの比は4:5なのだから、
A=④、B=⑤とする。
次に、BとCの比は3:4とある。
これをかけ算の式に書き直してみて。
B× \(\displaystyle \frac{4}{3}\)=C
ですね。保護者さまへこれが即答できない生徒がほとんどです。これは「暗記」事項なのです。ひらめきでもなんでもありません!しっかりと暗記させましょう。

あ、B=⑤だから、
⑤× \(\displaystyle \frac{4}{3}\)=○\(\displaystyle \frac{20}{3}\)
ですね。A=④、B=⑤、C=○\(\displaystyle \frac{20}{3}\)
だから、
A:B:C=4:5:\(\displaystyle \frac{20}{3}\)=12:15:20
大正解。
比は分数(のかけ算)にすぎないっていう基本を忘れないでね。
楽勝だよね。このタイプの問題を、分数のかけ算で処理しても、「連比」で処理してもどちらでも構わないよ。
ただね、「連比」ですっきりとまとめられる問題の方がやや多いかなあ。
もちろん分数のかけ算をした方がすっきり解ける問題だってある。
どちらでも解けることが大事だよ。
