比×比=比
今までは、文章題中に比が与えられている問題で、例えば4:3とあったならばそれぞれ④、③とおいて、解き進める問題をやってきました。
これとは別の、もう1つの比の活用があります。
どちらも、受験算数における大きな柱であり、必ずマスターしなければいけません。
これとは別の、もう1つの比の活用があります。
どちらも、受験算数における大きな柱であり、必ずマスターしなければいけません。
面積比
例題1
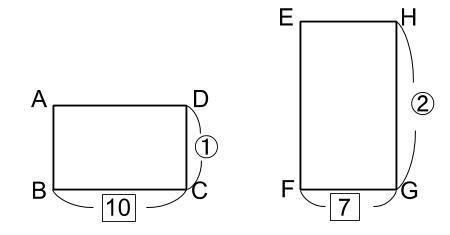
長方形ABCDのたての長さを2倍にし、横の長さを0.7倍にした長方形EFGHがあります。長方形ABCDと長方形EFGHの面積比を求めなさい。
解説

下図のようになっていますね。

長方形ABCDの面積=1×10
長方形EFGHの面積=2×7
10:14=5:7
ですね。
簡単すぎて変な感じがしますけど・・・

正解です。
簡単でOKなんです。
(たての比)×(よこの比)=(面積比)
これが成り立つ。あたりまえだって思えるよね。
もちろん、
(底辺の比)×(高さの比)=(面積比)
だって成りたつよ。
高さが等しい図形の面積比

ところで、
2つの長方形があって、高さ(たて)が等しいとする。
このとき2つの長方形の面積比はどうなるだろうか。
もちろん、底辺(よこ)の長さで面積が決まります。

底辺(よこ)の比と面積の比が一致しますね。

そうだね。
どちらにも(×1)をしただけだからね。あたりまえだよね。
「あたりまえ」なこととして、暗記してくださいね。
それで、先ほどの例題なんだけど、下図のように解くのもよくやるかな。

同じ高さの長方形を利用しているんですね。なるほど。

ここでの話は、「図形」の問題を解くときの最大の武器なんだ。
図形分野でさまざまな利用方法を学習していくことになるからね!