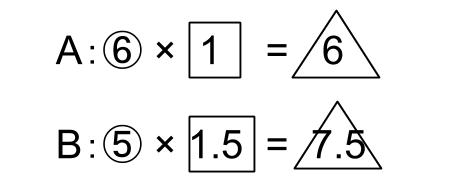【比】比と比の積・その1

習ってないからできませーんってこと、ないでしょ？

ＡもＢも買った個数は具体的に何個なのかはわからないけど、比がわかっていますね。
　
Ａ：100× １ ＝100
Ｂ：80× 1.5＝120　

100：120＝５：６かな。

うん、大正解。
感覚的にもこれで良いのが分かるよね。

別の説明をするならば、

Ａは a 個買った。
Ｂは（a×1.5） 個買った。
すると、

A：100× a＝100×a
B：80×（a×1.5）＝120×a　　　　　　

より、Ａ：Ｂ＝100×a：120×a＝５：６
となります。

この説明はちょっと数学的ですね。
感覚的にわかればOKです。

今度は、値段も個数も具体的な数値はわからないね。

さっきの問題と似てますね。ほとんど同じじゃないの？
値段の比が６：５だから、⑥、⑤として、
　
Ａ：⑥×１＝？
Ｂ：⑤×1.5＝？　　　

多分答えは、
（６×１）：（５×1.5）＝６：7.5＝４：５

４：５です。

うん、正解。
４：５でOKです。

答えはわかるんだけど、計算式がかけないんですよ。
　
Ａ：⑥×１＝６？
Ｂ：⑤×1.5＝7.5？　

６円と7.5円ってわけじゃないから・・・

うん、よく考えているね！
⑥円が１個なら⑥円
⑥円が２個なら⑫円
⑥円が３個なら⑱円
だよね。

でも、
⑥円が１個ならいくらになるのか。
確かにわからないよね。
わからなくて正解なんだよ。

？わからないのに正解？

うん。

⑥円が１個でいくらなのか。

その値段は、○でも□でも表せないんだ。

だから、このようなときは新しい記号を使うんだ。

例えば上の例なら、□と○をもう使っているよね。だから、新しく△とかおくんだ。

ああ、そういうことか。
また新しく記号を増やさないといけないのか・・・

でもね、ここまでていねいに毎回式をかかなくてもいいよ。
比はかけ算して、それがそのまま比になるって感覚があればそれでＯＫなのです。
だからこの問題も、いちいち△とか記号をおかなくてもいいよ。
かけ算した値をそのまま比にして、４：５がわかればそれでＯＫです。