比とは分数と同じもの。比とは分数の別名のことです。その表示方が違うだけのものだからです。
比とは何かを学ぶ
- 比の導入
-

今日は「比(ひ)」をやるよ。

いよいよ比ですね。
比が中学受験算数の最大の山場だと聞いたことがありますっ!!
どこで聞くの?

なんか友だちが言うんですよ。比がどうのこうの。
比で解くと簡単だとかなんだとか。
その友だちはすでに塾で比を習っているみたいだね。
比が中学受験算数の最大の山場っていうのは確かによく言われるかな。
やる気と不安でドキドキしますっ!

うん、頼もしいね。
新しいことを学ぶ意欲を感じるよ。
でもね・・・
比について、特に新しく教えることはないんだよ。
えっ?そうなの・・・

「比」を訓読みしたら「比べる」だ。
「比」とはね、2つの量を比べるだけなんだよ。
比とは何か、という小難しい説明よりも、具体例を見たら一発だ。
とにかく、見ていこう!
- 数量を横に並べれば比
-

Aが600円
Bが800円のとき、
AとBの所持金の比は
600:800(600たい800と読みます)これだけです。簡単すぎてびっくりだ!!

え・・・???これだけ???
えーーっ?
うそぉー!
横に並べただけですよ。
1年生の足し算より簡単じゃないですか!!!
比というのは本質的にはこれだけなんだよ。
2人の身長の比、2人の体重の比、いろいろな数量を比にできるよ。なんだか物足りなそうだね。
面倒な計算とかないと嫌かな?
えっと・・・嫌じゃないです。
楽なのがいいです。
でも、これだけって言われて、変な感じがします。
なんなんですかこれ?
ずばり比とは何か教えると、
比は分数(のかけ算)と同じものなんだ。横に並べれば比、たてに並べれば分数。
これが究極の答え。
Aが600円、Bが800円のときAの所持金はBの所持金の \(\displaystyle \frac{600}{800}\) である。
AとBの所持金の比は600:800
どちらも同じ意味なんだよ。
2つの表し方があるのです。
保護者さまへ
こちらは受験テクニックではなくて、数学的真実です。

それで・・・?

それでは計算をやりたくてウズウズしているみたいだから、計算をやってもらおうかな。
比はね、もっとも簡単な整数の比に直すのが普通なんだ。
分数は約分するよね。
\(\displaystyle \frac{600}{800}\) を約分すると?

\(\displaystyle \frac{600}{800}=\displaystyle \frac{3}{4}\)
です。

比も分数と同じように
600:800=3:4
とする。
比は、分数を約分するように、最も簡単な整数の比にします。
比と分数は同じものなんだと説明したよね。
それならば、比も「約分」するのは当然だよね。600:800=3:4
このように2つの等しい比を等号で結んだものを比例式というよ。

分かりました。
もっと知りたいんでどんどん教えてください。
うん、でも終わりなんだ。
もう新しいことなんてないよ。
「比」は「分数」と同じ。
横かたてか、並べ方が違うだけ。
これ以上ないよ。
え???これだけ?
比って結局何なのですか?
2つの数量が、互いに何倍なのかを表すための表現方法の1つが「比」です。
Aが600円で、Bが800円のとき、
AはBの \(\displaystyle \frac{3}{4}\) 倍だし、
BはAの\(\displaystyle \frac{4}{3}\) 倍だよね。
このような数量関係であることを示すための、新しい書き方が
「AとBの比は3:4」今まで「分数」で表現していたことの、”言いかえ”ということ。
ただそれだけだよ。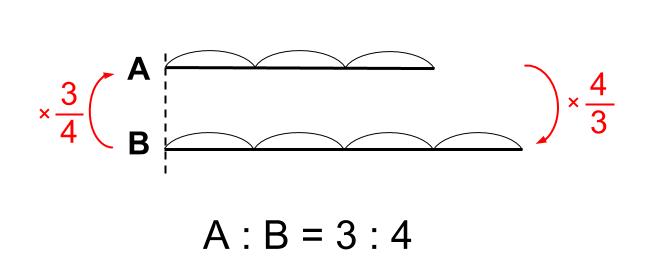

なんで「比」と「分数」と2つあるんですか?
どっちか1つでもいい気がしますけど。
そうだね、なんでだろうね。
でも同じ事柄に対して何通りも異なる表現方法があるってよくあることだよ。
「分数」で表現したり、「比」で表現したり、そんなもんだよ。
そんなもんですかね。

うん。あと、細かいことをいうと「比」ならではの新しいことがあるといえばある。
保護者さまへ
こちらは連比のことです。次の章で学習します。

なんだ、あるんじゃないですか。
はやく教えてください。
「比は分数(のかけ算)と同じ」
これこそが強く強く強く伝えたいことなんだよ。
まずはこれを確認したいから、新しいことはとりあえずおあずけしときたい。
はい、「比は分数(のかけ算)と同じ」
心得えておきます。例題に挑戦
- 例題1
-
- (1)Aが450円、Bが750円持っているとき、AとBの所持金の比をもっとも簡単な整数の比で求めなさい。
- (2)太郎は分速80m、次郎は分速60mで進んでいます。太郎と次郎の速さの比をもっとも簡単な整数の比で求めなさい。
- 解説
-
(1)450:750=3:5
約分と同じ、150で割ればOKです。(2)80:60=4:3
約分と同じ、20で割ればOKです。- 例題2
-
下の□に適切な値をいれなさい。
- (1)9:12=12:□
- (2)6:5=□:4
- 解説
-
(1)9:12=12:□
等号(=)の左を3で割れば、
9:12=3:4=12:□
つまり、3:4=12:□
なので、
等号(=)の左を4倍して、
3:4=12:16
□=16(2)6:5=□:4

代表的な解き方が3つあります。すべて覚えておきましょう。
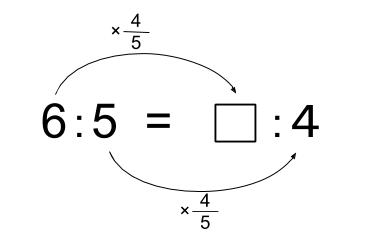

等号(=)の左を0.8倍(\(\displaystyle \frac{4}{5}\) 倍)しているという解き方。
つまり、□= \(6×\displaystyle \frac{4}{5}=\displaystyle \frac{24}{5}=4.8\)
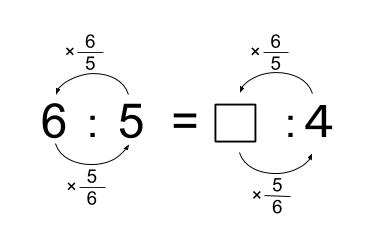

\(6:5\) なんだから、互いに\(\displaystyle \frac{5}{6}\) 倍、\(\displaystyle \frac{6}{5}\) 倍になっているという解き方。
つまり、□= \(4×\displaystyle \frac{6}{5}=\displaystyle \frac{24}{5}=4.8\)
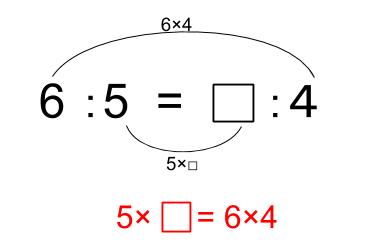

これははじめて教えることだけど、
比例式の、「内側どうしの積と外側どうしの積は等しい」という解き方。\(6×4=5×□\)
より、
□=\(\displaystyle \frac{24}{5}=4.8\)どの解き方も重要だから、しっかりと覚えておこうね。
- 例題3
-
下の比をもっとも簡単な整数の比になおしなさい。
- (1)\(\displaystyle \frac{5}{6}\) :\(\displaystyle \frac{3}{4}\)
- (2)\(\displaystyle \frac{14}{15}\) :\(2\displaystyle \frac{5}{8}\)
- 解説
-
(1)\(\displaystyle \frac{5}{6}\) :\(\displaystyle \frac{3}{4}\)
通分して分子を見比べてみましょう。
\(\displaystyle \frac{5}{6}\) :\(\displaystyle \frac{3}{4}=\displaystyle \frac{10}{12}\) :\(\displaystyle \frac{9}{12}=10:9\)
\(10:9\) が求める答えです。(2)\(\displaystyle \frac{14}{15}\) :\(2\displaystyle \frac{5}{8}\)
通分して分子を見比べても解けますが、やや計算が面倒です。
どちらも共通の数をかけて(割って)簡略化しましょう。\(\displaystyle \frac{14}{15}\) :\(2\displaystyle \frac{5}{8}\)\(= \displaystyle \frac{14}{15}\) :\(\displaystyle \frac{21}{8}\)
どちらの分子も \(7\) で割れますね。割りましょう。
\(\displaystyle \frac{14}{15}\) :\(\displaystyle \frac{21}{8}= \displaystyle \frac{2}{15}\) :\(\displaystyle \frac{3}{8}\)
あとは通分して分子を見ましょう。
\(\displaystyle \frac{2}{15}\) :\(\displaystyle \frac{3}{8}=\displaystyle \frac{16}{120} :\displaystyle \frac{45}{120}=16:45\)\(16:45\) が求める答えです。
- 例題4
- Aの身長は \(135.7cm\) で、Bの身長はAの \(95%\) です。AとBの身長の比を最も簡単な整数の比で表しなさい。
- 解説
-

Bの身長は、
135.7×0.95
うう、面倒だな・・・
そうだね、ちょっと面倒だね。
面倒なかけ算は「保留」しておく、というテクニックは知ってる?
135.7×0.95を135.7×0.95のまま扱うんだ。そのまま比を求めてごらん!
A:B=135.7:135.7×0.95
あ、135.7で割ればいいんだ。
A:B=135.7:135.7×0.95=1:0.95=20:19

はい正解!
面倒なかけ算は「保留」しておく、というテクニックも重要だから、しっかり覚えておいて欲しいのだけれど、この例題で学んで欲しいことは他にあるよ。
はじめから、135.7って数値はいらない情報でしたね。

大正解!
Bの身長はAの95%です。
とあるのだから、これこそがAとBの身長の比だよね。\(100:95=20:19\)
これだけでOKだよね。

