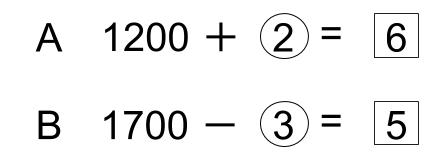異なる2種類の比の処理
共通部分がなく連比ができないパターン
例題
Aは1200円、Bは1700円持っていました。その後Aはおこづかいをもらい、Bは本を買いました。その結果、2人の所持金の比は6:5になりました。AがもらったおこづかいとBの買った本の金額の比は2:3です。このとき、本の値段はいくらですか。
解説

Aは②もらって、6になった。
Bは③使って、5になった。

○をそろえるか・・・
□をそろえるか・・・
どっちにしようかな。

消去算は、〇をそろえても解けるし、□をそろえても解けるからね。
計算が楽そうな方を選べば良いのです!

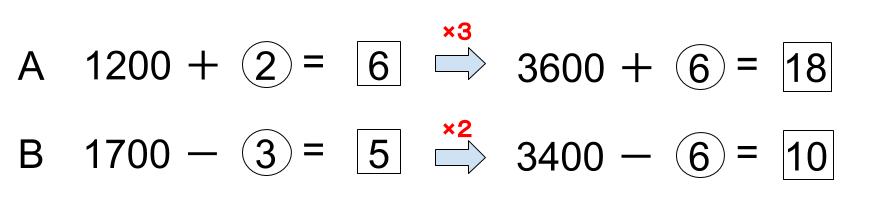
じゃあ、〇をそろえます。
〇を6にそろえます。

⑥がそろったけど、符号が「+」と「-」で違いますね。
このあたりの式処理が小学生には難しいところだよね。
このようなときは2つの式の差をとるのではなく、和をとるのです!
和をとると、「足す⑥」と「引く⑥」が打ち消しあって消えます!

言われてみればそうですね。
しっかり覚えておきます。
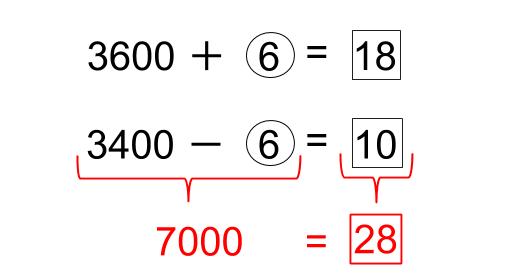
28=7000
だから、
1=250
つまり、
A:1200+②=1500
B:1700-③=1250
本の値段③は、1700-1250=450
450円ですね。
求まりました!

正解です!
そろえたものの符号(+と-)が異なる場合は、和をとって消すのです!
理解するのがベストだけど、とりあえず暗記でも良いでしょう!
Aの式の方も矛盾が起きていないことを確認しておこう。
A:1200+300=1500
B:1700-450=1250
②=300で、③=450
比がうまくいっているから矛盾なしですね。
別解

さっき、とても大事なことを教えました。
消去算は、〇をそろえても解けますし、□をそろえても解けます!
計算が楽そうな方を選べば良いのです!
ですから、□をそろえる別解も見ておきましょう。
やってみてくださいな。

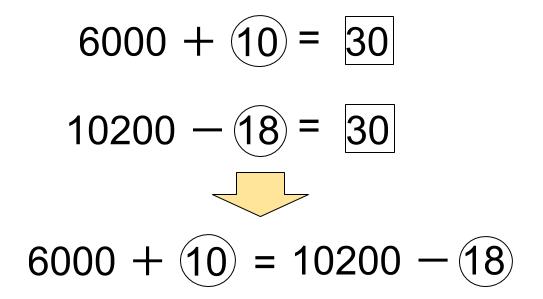
A:1200+②=6
B:1700-③=5
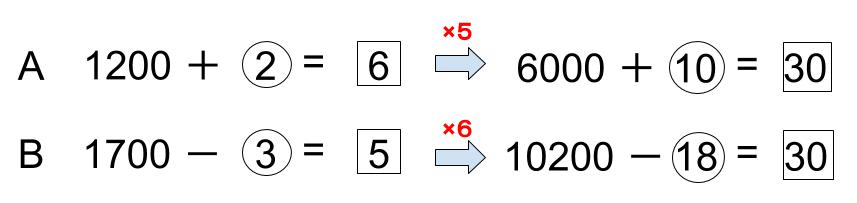
だから、30にそろえますね。

えっと・・・
和をとると解ける?
差をとると解ける?
符号が同じだから、差なのかな?

はい!良いですね。
今回は差をとることで解決ができます。
しかし・・・
この2つの式の差をとるのも、小学生にはちょっと厳しいかな・・・
できるならそれでOKなんですけどね。
このようなときは、2つの式を等号(=)で結ぶのです。

どちらも30で等しいのか。なるほど!
で・・・続きはどうするんだ??

「1つの記号しかない等式」が1つあるわけですね。
このようなときに何をすればいいのか・・・
これは考えることじゃなくて、知っているかどうかの話だ。
「等式」については以前にがっつり教えたのだけどな。
絶対に忘れてはいけない計算技術ですよ。

等式ですか。あらためて教えてください。

等式は、より簡単になるように変形するのです。
変形の仕方は、「等号の左右に同じ計算をする」
これだけです。
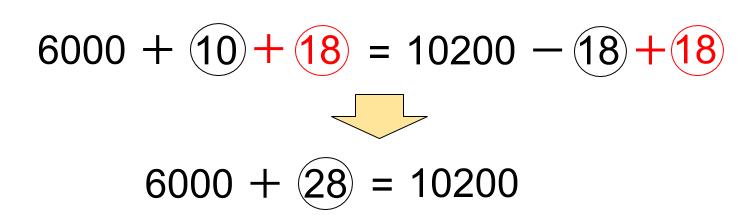
今回なら、例えば、左右に⑱を足してみよう。

あ!〇28が、10200-6000=4200だとわかります。
4200÷28=150
つまり、①=150円だ!
③=450円。
本の値段が求まりました。

その通りです。
とにかく計算のルールを覚えて練習するだけです。
「文章題を整理していったら消去算になった」というケースは今後たくさん出てきます。
そのときに計算技術がないせいで問題が解けないのは最悪です。
「ただの計算」なので、この消去算は必ずマスターしておかないといけません!