異なる2種類の比の処理
異なる2種類の比の処理の練習
例題
持っていたお金の \(\displaystyle \frac{3}{7}\) より200円安い商品Aを買った後、残りのお金の \(\displaystyle \frac{2}{5}\) より300円高い商品Bを買ったところ、はじめの30%のお金が残りました。はじめいくら持っていましたか。
解説

残ったお金の・・・と話が続くパターンは、線分図を2、3段階にかいていくパターンでしたね!

そうだね。
その情報整理がダントツにおススメですよ。
よく覚えていたね!
では図をかいてみてください。
ちょっと複雑だから、大きめにていねいに書いていこうね。

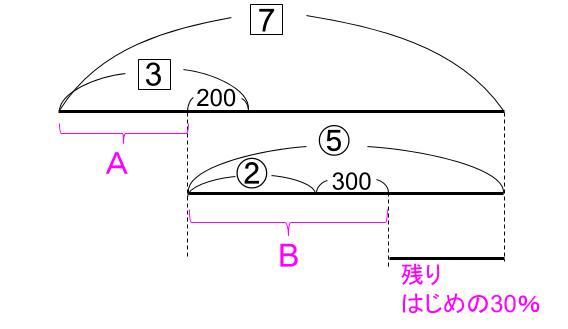
下図のような感じですかね。

上手にかけたね。
ここからの考え方はいつもとまったく同じ。
〇と□の2つの異なる比があるのだから・・・
1.共通部分があればそろえる
2.なければ、等式を2つつくって消去算

共通部分は・・・なさそうですね。
等式を2つつくります。

では線分図をよく見てね。
等式は「つくる」というよりも「探す」んだよね。
この問題において、何と何が等しいのかを探すわけだ。

残りのお金が2通りでかけますね。
③-300
と
はじめの7の30%で、
7×0.3=2.1
だから、
2.1=③-300
あとは・・・えっと・・・

問題の情報は全部使わないと解けないよ。
商品Aが関係する所でもう1つの等式をつくりましょう。

商品Aを買ったあとの残りは、4+200
そして、この残りを⑤とおいた。
つまり、
4+200=⑤
あとは消去算をすれば求まりますね!

OK!
しっかり計算を最後までやりきってね!

2.1=③-300
4+200=⑤
□よりも○の方がそろえやすいかな。

⑮にそろえようとしてる?
間違いではないけれど、
2.1=③-300
を3で割って、
0.7=①-100
を使おうね。

なるほど!そうします。
0.7=①-100
4+200=⑤
⑤にそろえますね。
3.5=⑤-500
4+200=⑤
で・・・2つの式の差をとると・・・?
あれ、わからないな。

等式の変形を利用して、計算のやりやすい形にするんだ。
3.5=⑤-500
の左右に500を足すと、
3.5+500=⑤
となるね。

等式の変形ですね。なるほど。
で、
3.5+500=⑤
4+200=⑤
だから、
3.5+500=4+200
ここでも等式の変形ですね。左右から200を引けば、
3.5+300=4
つまり、0.5=300
はじめは7持っていたのだから、
7=4200
求まりました!
4200円です。

正解です!
けっこう複雑な式処理だけど、ルールはいつも通り。
よく練習をしておきましょうね。

別解も紹介しておくよ。
商品Aを買って、残りなんだけど、
4+200
ここで、この残りを⑤とはせず、そのまま計算をすすめる。
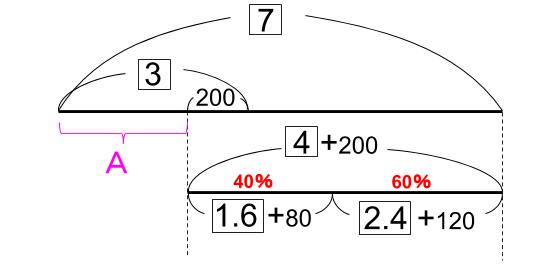
残り4+200 の\(\displaystyle \frac{2}{5}\) (0.4)倍は、
(4+200)×0.4=1.6+80
同様に、残りの\(\displaystyle \frac{3}{5}\) は2.4+120

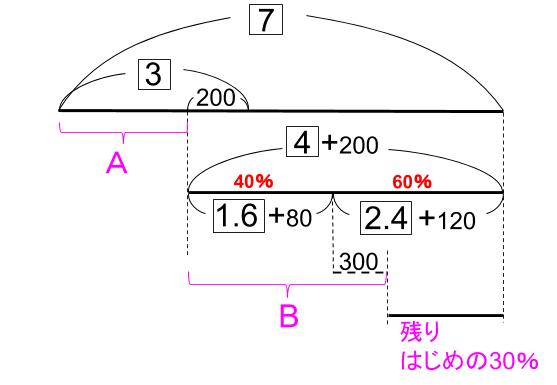
「商品Bは、残りのお金の \(\displaystyle \frac{2}{5}\) より300円高い」なので、
下図のようになります。

残りは、
2.4+120-300
だから、
2.4-180
そして、はじめ7の30%でもあるから、
残りは、2.1
2.4-180=2.1
ですね。
つまり、0.3=180
1=600
7=4200
これが答え!
はじめのお金です。求まりました。
こっちの方が簡単かも!!