異なる2種類の比の処理
連比
例題1
所持金について、AはBの \(\displaystyle \frac{4}{5}\) である。また、BはCの \(\displaystyle \frac{3}{4}\) である。このとき、AとCの所持金の比を求めなさい。
解説

これ、覚えているよね。復習だよ。
楽勝で解けないとまずいよ。

はいやってみます。
あ、連比ですね。解けました。
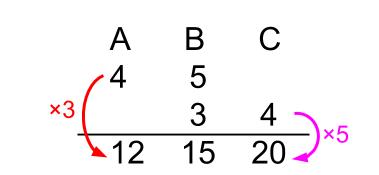
A:C=12:20=3:5です。

うん、これは復習だからね。この基本がまずは分かっていることが前提なんだ。
A:B=4:5
つまり、Aは④、Bは⑤とおける。
また、
B:C=3:4
つまり、Bは3、Cは4とおける。
2つの異なる比、つまり2種類の記号がでてきたら・・・
今回なら〇と□だけど。
B=⑤=3
のように2つの比の共通部分を公倍数でそろえて、1つの比(1つの記号)ににしてしまうのが連比という解法だったよね。
この当たり前の事実を復習した上で、さらに深く比について学んでいきますよ。
さっそく次の例題をやってみよう!
消去算
例題2
ある学校の入学試験で、180人が合格、90名が不合格となりました。男子の合格者と不合格者の比は16:9であり、女子の合格者と不合格者の比は7:3でした。男子の合格者は何人でしたか。
解説

さっそく「2つの異なる比」ですね!
男子の合格者は⑯
男子の不合格者は⑨
女子の合格者は7
女子の不合格者は3
とおけます。
2つの比の共通部分を見つければ良い・・・
あれ?
見つからないな・・・わからないです・・・

はい。わからなくてOKです。
実は、常に2つの比の共通部分が見つかるわけではないんです。
「2つの比の共通部分がない」タイプの問題もあるんです。
そのようなときは、どうするのか。
今から教えますからね。

そうなんですか。
どうりで見つからないわけだ。

「2つの比の共通部分がない」タイプの問題の解き方は、
ずばり!
「2つの等式をつくって消去算」をする。
これで決まりです!
実際にやってみないとピンとこないから、どんどんやっていきましょう。
この問題では、もちろん合格者が180名と不合格者が90名という情報も使うはずだよね。
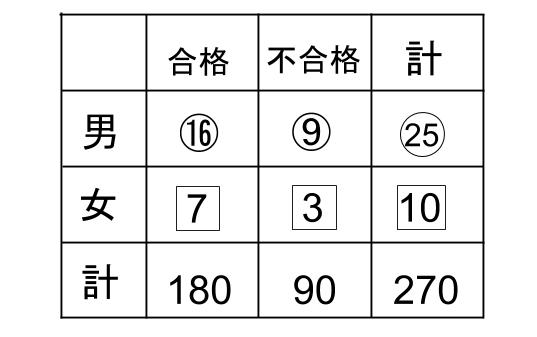
等式をつくるためにも、情報整理をしておきましょう。
下図のようにまとめるのがおススメですね。

2つの等式がつくれますね。
⑯+7=180
⑨+3=90
となります!

続きはどうやるか、もうわかって欲しいのですが・・・
「消去算」ですよ。
覚えてますか?

えっと、最小公倍数でそろえて差をとります!
□をそろえて解いてみますね。

うん、覚えているみたいで良かった。
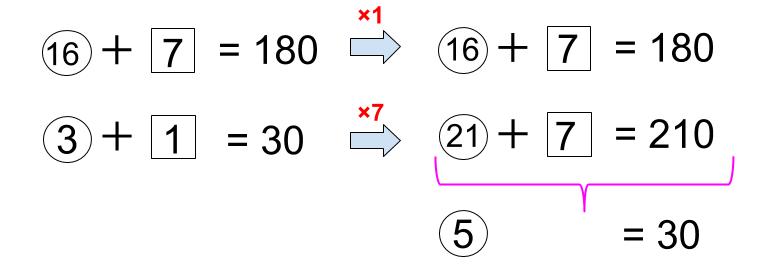
それで、最小公倍数にそろえる前に、
⑨+3=90
を3で割って、
③+1=30
を利用した方が計算が楽だよ。

えっと、最小公倍数でそろえて差をとります!
□をそろえて解いてみますね。

⑤=30ですね。
ということは、
①=6なので、男子の合格者⑯=96
求まりました!
96人です。

はい、正解です!
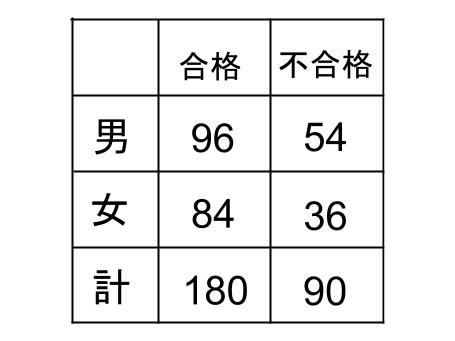
男子の合格者以外の数値もすべて求まりますね。

この問題を解く上では使わなかったけど、情報のまとめ方として、下図のように
男子だけの合計、女子だけの合計の欄を使うこともよくあるから覚えておいてね。

あとね、消去算についても豆知識。
さっきは、□を7にそろえて解いたよね。そして、もちろん○の方をそろえて消したって解けることは知っていると思う。
さらにね、「数値をそろえたって解ける」ということも見ておこう。
普通はこの解き方を選ぶことはないけどね。
はじめから数値がそろっているときはこの解き方をするのもありだからね。
「数値をそろえたって解ける」は知っておくべきなんだ。

180となる2つが等号(=)で結ばれた。
⑯+7=⑱+3
ここから先は「等式の変形」
これももう身についていますよね?
左右どちらからも、⑯を引いてみると、
7=②+3
さらに、左右どちらからも、3を引いてみると、
4=②
左右を2で割って、
2=①
異なる2つの比が等号で結ばれましたね。
これを用いて、1つの記号だけの式で今までの情報を書き直せば解けますね。

あれ?
この問題は、「2つの比の共通部分が見つからない」タイプだったはず・・・?
2=①
って見つかりましたね。

まあね。だから厳密に言い直せば、
「2つの比の共通部分が、消去算をしないと見つからないタイプ」ってことですかね。