食塩水と面積図
食塩水混合と面積図
例題4
濃さが16%の食塩水と濃さが6%の食塩水をまぜたところ、濃さが12%の食塩水が600gできました。濃さが16%の食塩水は何gまぜましたか。
解説

これも面積図ですね。
図はこうなりますね。
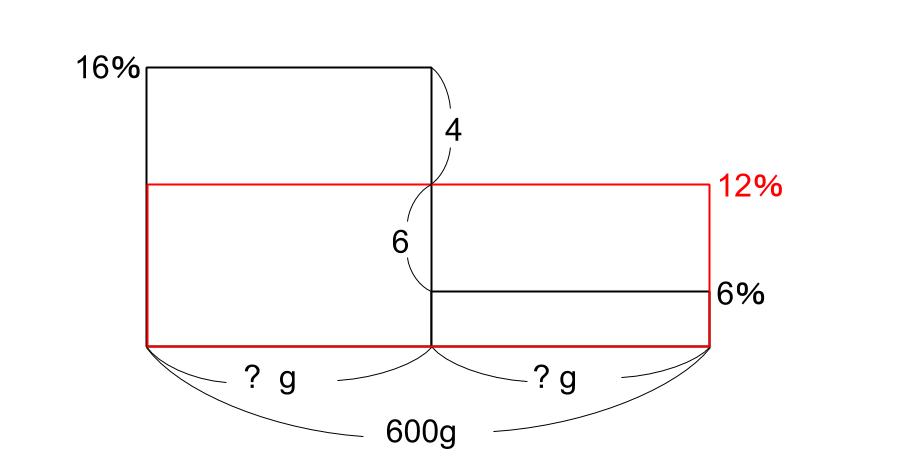

とび出た長方形とへこんだ長方形の面積が等しい。
えっと・・・逆比だ!
4×③=6×②
で等しい。
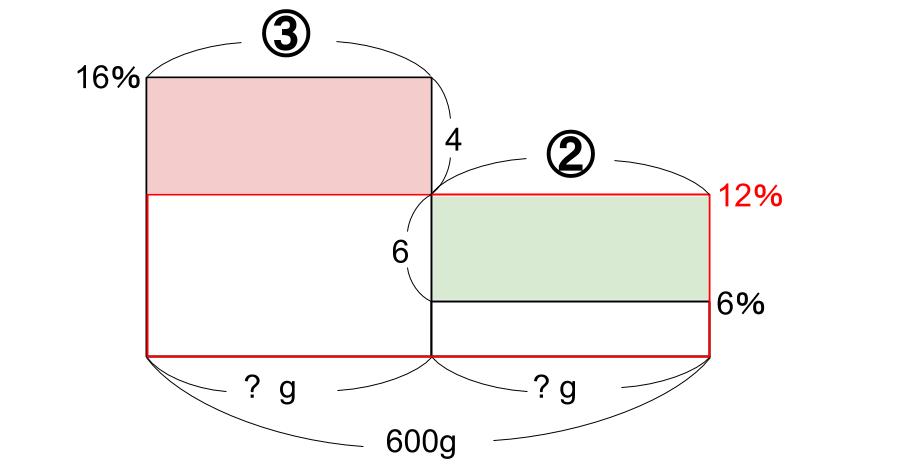

③+②=⑤
これが600gにあたるから、
①=120g
16%の食塩水は③gだから、
360gです。
求まりました。

大正解!
言うことなしですね。
ちなみにさ・・・
この問題は「つるかめ算」でもあるのだけど、言われたらわかるかな?

?突然すぎて・・・え?つるかめ算?
あまりにも無関係なものがでてきてびっくりです。

つるかめ算だって「面積図」でしょ。
実は無関係でもないんだよ。
平均をとらないで、面積がいくつなのかに注目してごらん。
今回は、「面積=食塩の量」だ。
まぜたあとの食塩水から食塩の量がわかる。
600×0.12=72
つまり、面積が72になるよって問題。
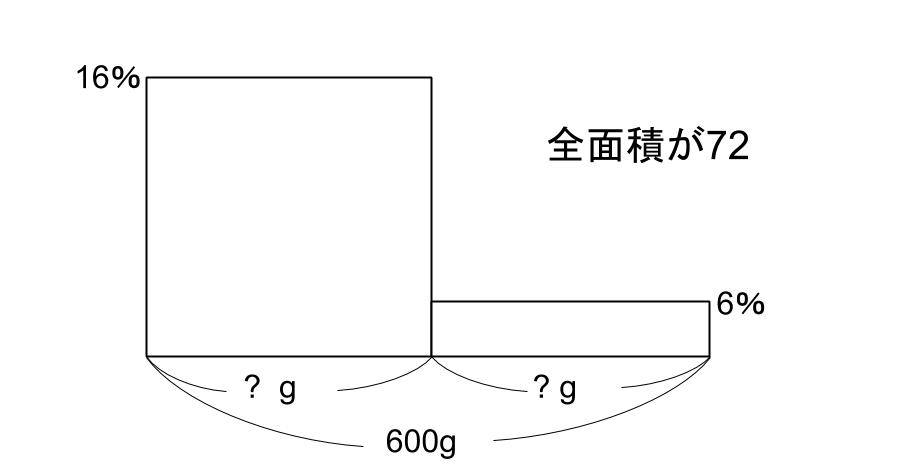

確かにつるかめ算ですね。
もし全部6%なら、
600×0.06=36
72-36=36
36÷(0.16-0.06)=360
さっきと同じ答えが得られました!

うん。そういうことです。
1gにつき0.16gの食塩がとけているA
1gにつき0.06gの食塩がとけているB
AとBがあわせて600gいます。食塩は全部で72gです。
Aは何gですか。
こう書いたらつるかめ算そのまんまになるね。

なるほど。
ところで、この問題は、つるかめ算のように解いた方がよいですか?

いや、別にどう解いたってかまわないよ。
深く理解するために紹介しただけです。
保護者さまへ
ここまでの話で、「あれ?では逆につるかめ算って平均でも解けるの?」という疑問を持つ子もいます。まったくその予想は正しく、つるかめ算を平均として解くことができます。
ちなみに、このような疑問を持つ子はほとんどいません。極めて聡明で算数向きの頭をしている子だけです。
