【食塩水】食塩水の複数回移動・その4

さっきと同じ？に見えますね・・・何か違うのかな？

とにかくやってみますね。
途中の濃さは求める必要はない。
食塩水全体の量と食塩の量だけを追いかける！

100ｇくみだしたから、
250ｇで濃さ9.5％、とけている食塩は
250×0.095=23.75（ｇ）

で、次に水を130g入れる。

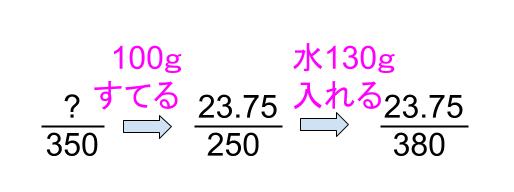
ここから220ｇ捨てるから、残りは160g
そこにとけている食塩の量は、

23.75×\(\displaystyle \frac{160}{380}\)

えー、計算面倒だよおおお！！

　
そうだね。確かにちょっと面倒だね。
でも面積図を使って計算が楽になるわけでもないよね。
計算せよ！

そうですかね・・・

23.75×\(\displaystyle \frac{16}{38}\)=10

あ！めちゃくちゃきれいになった！
19で約分できたぞ。

あとは簡単ですね。
下図のようになるから・・・

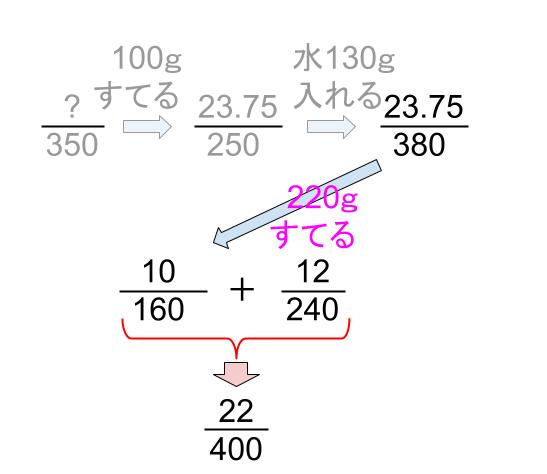
400ｇでとけている食塩は22g

つまり濃さは、

\(\displaystyle \frac{22}{400}\)×100=5.5

5.5％ですね。

ＯＫ！正解。
とてもうまく解けていたよ。

そして、ここでさらなるコツを伝授するよ。

今回は、食塩の量を求める計算が面倒だったね。

23.75×\(\displaystyle \frac{160}{380}\)

も嫌だけど、はじめの
250×0.095=23.75
だって計算がちょっと面倒だよね。

はい。

だからさ、こんなときは「計算しない」んだ。
250×0.095は、いくつになるのか計算しない。
（250×0.095）のまま扱うんだ。

少し変形して、（25×0.95）とか（2.5×9.5）とかで扱ってもいい。

とにかくこの計算をする必要はない。

え？計算を途中でやめておくの？

そうだよ。かけ算は最後までやらないで、保留しておくのがコツ。
その後さらに続きのかけ算があるならば、そこで約分ができる可能性がある。
約分もせずに途中経過を計算しても、ただの無駄になる可能性が高い。
（2.5×9.5）を使って、もう一度解いてみてごらん。

そうなのかな。とにかくやってみますね。
水を130ｇいれるところまでは下図。

ここから220ｇ捨てるから、残りは160g

この160ｇにとけている食塩の量は、

2.5×9.5×\(\displaystyle \frac{160}{380}\)

あ！なるほど。
38=19×２で
19=9.5×２

だから、9.5で約分できるって、すぐにわかります！

　
その通り！
かけ算は最後までやらないで、保留しておくのがコツ。
なぜならば、

・かけ算をしないで済む
・あとで約分するときに公約数がみつけやすい！

この「かけ算を保留するテクニック」は食塩水に限った話じゃないからね！
いろいろな問題で使えるから必ず活用しようね！