【食塩水】食塩水の複数回移動・その2

面倒そうだな・・・・
８％の食塩水200g →８％の食塩水150g
　　
８％の食塩水150gと水100gで　→　?％の食塩水250g

？％は面積図なしでも求まりますね。
150×0.08=12
12ｇの食塩が解けている250ｇの食塩水の濃さは・・・

間違ってはいないけどさ、その濃さは求める必要がないでしょ。
途中経過の濃さなんて、いちいち求める必要はないのだから。

略図で整理してみよう。
まず、８％の食塩水200g から50ｇを捨てる。
当然残りは150gになる。

この食塩水150gにとけている食塩が12ｇはどうやって求める？

濃さははじめと同じ８％ですから、
150×0.08=12

正解。
もう１つ、別の求め方は？

え？えっと・・・

200gあった食塩水のうち、150ｇが残った。

つまり、 \(\displaystyle \frac{150}{200}=\displaystyle \frac{3}{4}\) 残っているのだから、

とけている食塩も \(\displaystyle \frac{3}{4}\) となる。

16×\(\displaystyle \frac{3}{4}\) =12

こちらのやり方も絶対にマスターしないとダメだよ。

では続き。

水を100ｇ入れてまぜて、50ｇすてる。

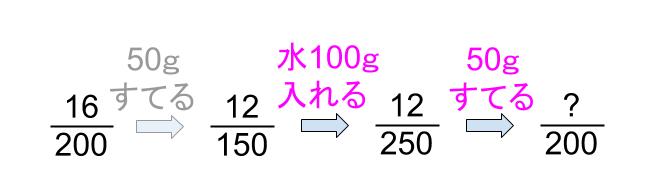
とけている食塩の量「？」を求めてくださいな。

１つ前の、
「全体が250ｇで食塩12ｇの食塩水」の濃さと同じですね。
50ｇ捨てる前と後で、濃さは同じですからね。

\(\displaystyle \frac{12}{250}\)×100=4.8(％)

全体が200ｇで濃さが4.8(％)だから、とけている食塩の量は

200×4.8＝9.6
9.6gです。

間違ってはいないけど、「濃さ」なんて出す必要ないってば。

250ｇのうち、200ｇ残ったのだから、\(\displaystyle \frac{200}{250}\) 残った。

だから、とけている食塩も \(\displaystyle \frac{200}{250}\) 残る。

12× \(\displaystyle \frac{200}{250}\) =9.6

よって、9.6ｇの食塩がとけているのです。

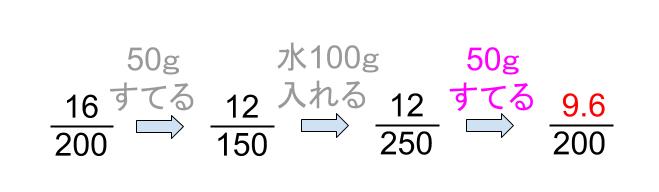
最後、ここに水を100ｇいれると・・・

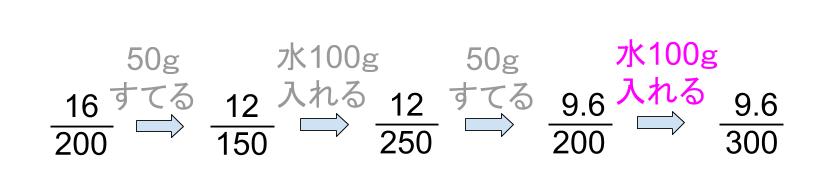
300ｇに9.6ｇがとけている。

\(\displaystyle \frac{9.6}{300}\)×100=3.2(％)
　
濃さは3.2％だ！

正解です。
とにかくポイントは、途中の「濃さ」を求める必要はないということ。
「食塩水全体の量」と「とけている食塩の量」がどのように変化していくのかをていねいに追いかけるんです。

なるほど。
よくわかりました！

ところで先生。

この分数のような表示、分数じゃないよって言われましたけど、

分数として見れば、「食塩水の濃さ」そのものを表していますよね。

\(\displaystyle \frac{食塩の量}{全体の量}\)✕100

ですからね。

百分率になおすために100倍するかしないか、それだけの違いです。
最後の濃さを求めるときに気づきました。

あら、よく気がついたね。

あまり教えすぎて混乱させるのも嫌だから言わなかったんだけどね。

「途中の濃さを求める必要はない」と教えてきたけど、厳密に言い直せば、

「途中の濃さを百分率に直す必要はない」

ということなんだよね、実は。