損益
複数の商品・比の活用
例題
ある商品を何個か仕入れました。原価の5割増しの定価で \(\displaystyle \frac{2}{3}\) が売れ、残りは定価の2割引きですべて売れました。全体の利益は何%ですか。
解説

値段も個数も、具体値は一切なしですね。
好きな数値で解いてしまいますね。

はい、それでOKです。

では、1個100円のものを、3個仕入れたとします
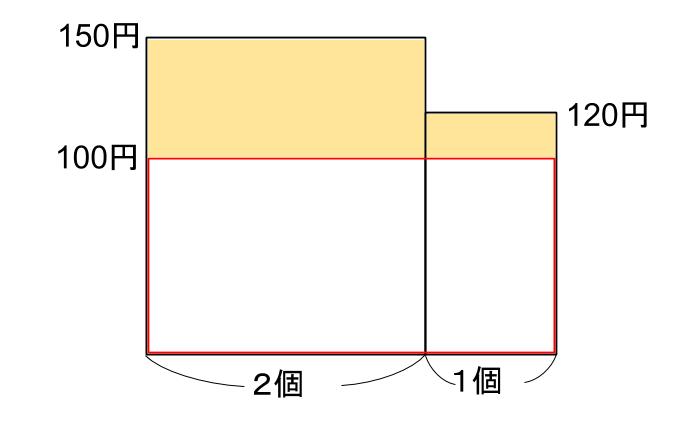

クリーム色の面積が利益なので、
50×2=100
20×1=20
100+20=120(円)の利益
原価の総額は、100×3=300
利益120円は、原価300円に対して4割=40%
求まりました。
40%です。

OK!正解です。
平均との関係性

別解です。平均との関係にもふれておきましょう。
「全体の利益」という言葉ですが、これは「平均」とほぼ同じ言葉です。
「原価の5割増しの定価で \(\displaystyle \frac{2}{3}\) が売れ、残りは定価の2割引きですべて売れると、平均で利益が何割か?」
という問題ということです。
平均の面積図は次のようになります。
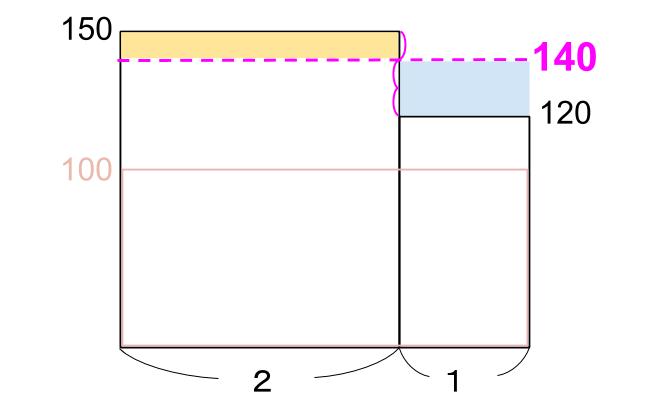

平均して4割の利益であることがわかります。
平均と同じことを言っている問題なのでした。
※今までの他の問題も、平均と同等の問題はたくさんあります。
比と具体値の関係性

今回のように、「比・割合」しか与えられてなくても問題として成立します。
そこに「具体値」の情報を与えることで、今までの様々なパターンの問題が作れるのです。
具体例をみていきましょう。
参考例題1
ある商品を総額30000円で仕入れました。原価の5割増しの定価で \(\displaystyle \frac{2}{3}\) が売れ、残りは定価の2割引きですべて売れました。全体の利益をもとめなさい。

仕入れ値の総額30000円が与えられました。他は先の例題と同じです。
つまり、「全体の利益は40%」になることは、仕入れ値の総額30000円とは無関係に決まる事実です。
ですから、30000×0.4=12000
全体の利益は12000円となります。
参考例題2
ある商品を300個仕入れました。原価の5割増しの定価で \(\displaystyle \frac{2}{3}\) が売れ、残りは定価の2割引きですべて売れました。全体の利益は6000円でした。この商品1個の原価をもとめなさい。

仕入れた個数300個と、全体の利益6000円が与えられました。他は先の例題と同じです。
つまり、「全体の利益は40%」になることは、今回も与えられた具体値とは無関係に決まる事実です。
ですから、6000÷0.4=15000
仕入れ値の総額は15000円です。
仕入れた個数は300個なので、
15000÷300=50
1個の原価は50円です。
