損益
複数の商品・比の活用
例題
ある商品を何個か仕入れたところ、仕入れ値の総額は8000円でした。仕入れ値の5割増しの値段で仕入れた個数の \(\displaystyle \frac{3}{4}\) が売れましたが、残りは最後まで売れ残りました。全体の利益はいくらですか。
解説

商品1個の原価も、何個仕入れたのかもわからないですね。
1個の仕入れ値が①円の商品を、100個仕入れて総額が8000円。
うーん、これでいいのかな??

○数値と□数値をかけ算するのは嫌だよね。
嫌だって思ってくれているよね?
①が5個あれば⑤
①が20個あれば⑳
これはわかりやすいよね。
でも、①が1個あるとき・・・
①×1がいくつになるのかってピンとこないよね。
①×1の値は、〇でも□でもない別の記号をおかないといけないんだ。
実はこのやり方でも解けるんだけど、小学生にはこの後の式処理がかなり難しい。
だから別の解き方をおススメします。
こういうときの解き方のポイントをずばり教えますよ!

何個仕入れたのかわからない。
何個売れたのかわからない。
何個売れ残ったのかわからない。
最後の最後まで個数に関する具体値が出てこないでしょ。
こういう問題では、個数を勝手に決めてしまってかまわないんだ。
例えば、
100個仕入れたと勝手に決める。
仕入れ値の総額は8000円なのだから、1個の原価は80円と決まります。
これで解き進めれば正しい答えがでます。
あるいは、
4個仕入れたと勝手に決めます。
すると、1個の原価は2000円と決まります。
これで解き進めても正しい答えがでます。
どんな値でもOKです。勝手に決めてしまってかまわないよ。

?え・・・そうなの?
そんな勝手なことしちゃっていいの??

さっきも言ったとおりだけど、個数に関しては最後まで具体値がないでしょ。
そういうときは勝手に決めてしまってかまわないんだよ。とにかく解いてごらん。

「1個の原価が2000円を4個仕入れた」で解くと、全仕入れ値は8000円。
仕入れ値の5割増しで仕入れた個数の \(\displaystyle \frac{3}{4}\) が売れたから、
3000円で3個売れた。つまり売り上げは9000円。
残り1個は売れなかった。
結局、8000円で仕入れて9000円の売上。
利益は1000円です。
では次。
「1個の原価が80円を100個仕入れた」で解くと、
全仕入れ値は8000円。
75個が120円で売れた。つまり売り上げは、75×120=9000(円)
残り25個は売れなかった。
結局、8000円で仕入れて9000円の売上。
利益は1000円です。
あ、本当だ・・・どっちで解いても同じ答えがでますね。
答えは1000円ですか?

はい、1000円で正解ですよ。
しっかりこの解き方を覚えてくださいね。

ちなみに・・・1個の原価がいくらであっても、必ず同じ答えがでることの説明をしておこうかな。
「仕入れ値の5割増しの値段で仕入れた個数の \(\displaystyle \frac{3}{4}\) が売れた」
とは、仕入れ値と売値の比が2:3
売れた個数と仕入れた個数の比が3:4
次の面積図のようになります。
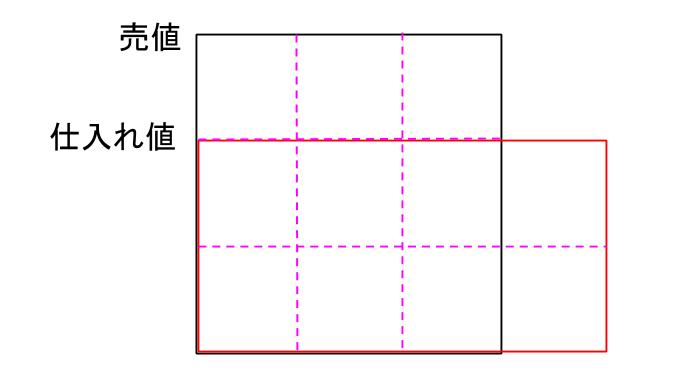

全仕入れ値は赤い長方形の面積で、小さい長方形8個分
全売り上げは黒い長方形で、小さい長方形9個分
全仕入れ値と全売り上げの比は必ず8:9になる。
これこそがこの問題の構造なのです。
具体的にいくらの商品だったのか、とは完全に無関係にこれが成り立ちます。

今回は、全仕入れ値は8000円。
つまり、小さい長方形1個が1000円なんですね。
これは100円が10個でも200円が5個でもなんでもいいと。
なるほど!

まあとにかく、「はじめから最後まで具体値がでてこないもの(値段・個数)には、具体値を勝手に決めて解いてよい」と覚えてしまってかまわないよ。
