ニュートン算・総量に着目する
- 例題9
- ポンプで満水の井戸水をすべてくみ出すのにポンプ5台だと8時間、ポンプ8台だと4時間かかります。ポンプ12台では何時間何分かかりますか。ただし、常に一定量の水がわき出ているものとします。
- 解説
-

ニュートン算は得意になってきたかな?

はい、いつもワンパターンで解けますからね。
そうだね。ワンパターンで解いてきたよね。
(はじめの仕事量)÷(1時間の仕事量-1時間のじゃま)=(時間)
という式を2本かいて、比で解くやり方を見てきたね。
もちろん、「1時間の仕事量」ではなくて、
「1分の仕事量」だったり「1日の仕事量」だったりする。
これらをまとめて、「単位時間あたりの仕事量」と言います。今までの解き方は、
「単位時間あたりの仕事量」に着目する解き方です。
はい、ワンパターンでした。
この解き方とは別の解き方もあるんだ。
ここからは、それについて教えることにします。
他の解き方ですか・・・
そうなんです。
もう1つの解き方は、「仕事をした総量」に着目する解き方なんだ。ニュートン算では、「はじめにある仕事量」に加えて、
時間とともにどんどん仕事が増えていくよね。水が入ってくる、人が並んでくる、草が生えてくる、などです。
これら「追加された仕事量」を「はじめにある仕事量」と合計して、「全部でどれだけの仕事をしたのか=仕事をした総量」に着目する解き方なんだ。

へえ・・・
「はじめにある仕事量」+「追加された仕事量」=「仕事をした総量」
なるほど・・・
とにかく具体例を見た方がはやいね。
さっそく例題でこの新しい解き方、「仕事をした総量に着目」を見ていくことにしよう。
では、問題を解いていきましょう。
・ポンプ5台だと8時間ですべてくみ出す。
・ポンプ8台だと4時間ですべてくみ出す。これらを整理していきます。
1時間で追加される仕事量(わき出ている水)を①
ポンプ1台が1時間でする仕事を1とおきましょうか。
・ポンプ5台だと8時間ですべてくみ出す。
「はじめの量」+「8時間でわき出した量」=「5台8時間のくみだし」1時間のわき出し量が①だから、「8時間でわき出した量」は⑧ですね。
ポンプ5台が8時間でくみ出した量は、5✕8=40つまり、
「はじめの量」+⑧=40
という式になります。
OKです。
次に2つめの条件だ。
・ポンプ8台だと4時間ですべてくみ出す。
1時間のわき出し量が①だから、「4時間でわき出した量」は④です。
ポンプ8台で4時間でくみ出した量は、8✕4=32つまり、
「はじめの量」+④=32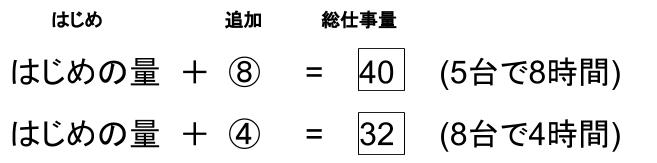

はい、うまくできてます!
あとは、この2つの式で消去算をすればいい。
「はじめの量」+⑧=40
「はじめの量」+④=32上の式から下の式を引けば、「はじめの量」が消えて、
④=8
これはもちろん4で割って、
①=2これを使えば、〇だけの式、あるいは□だけの式にすることができますね!
どちらでもいい。1つの記号にそろえましょう。
①=2で「はじめの量」+⑧=40
を□だけの式にすると、「はじめの量」+16=40
つまり、
「はじめの量」は、24であることがわかりました!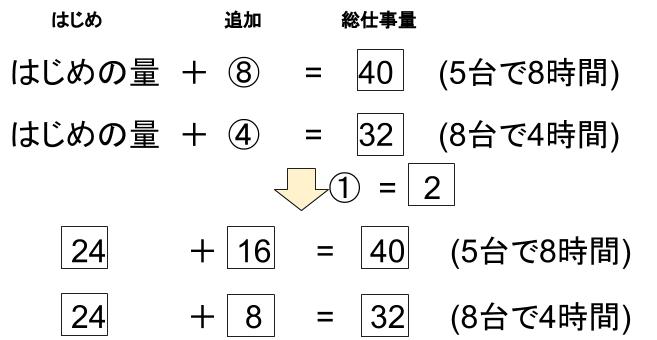

はい、上手に解けていますよ。
続きはどうかな?

ポンプ12台で仕事をするならば・・・「はじめの量24」+「?時間の追加(わき出し)」=「ポンプ12台が?時間でくみ出した量」
ポンプ1台が1時間でする仕事量は1
1時間のわき出し量は、①=2
なので、「はじめの量24」+「2✕?」=「12✕?」
?はえっと・・・

学くんの解き方でOKなんだけども、最後は普通に仕事算の式で解いた方が楽だよ。
「単位時間あたり」の解き方ね。
え?
途中で解き方変えるんですか?
今日はいつもと違う解き方するって・・・ブツブツ
1時間のわきだし量は、
①=2だから、ポンプ12台で仕事をすると、
「はじめの量24」÷(12−2)=2.4(時間)2.4時間は、2時間24分
求まりました!答えは、2時間24分です。
確かにこっちのほうが楽ですね。
はい、正解です。
最後は楽な方(単位時間)で解きましょう。

さて、「仕事の総量」に着目する解き方を見てきました。
しかし、この問題は今まで通りの解き方(単位時間)でも解けます。1時間あたりにどれだけ仕事が減っていくかの解き方です。
「はじめの量」÷(5-じゃま)=8時間
「はじめの量」÷(8-じゃま)=4時間
という2つの仕事算の式をかいて、式処理をしていく解き方ですね。
はい、わかります。
そっちの解き方は大得意ですから。
今までの解き方を、解き方1(単位時間)
今回の解き方を、解き方2(総量)
と呼ぶことにします。解き方1(単位時間)は、仕事がじゃまをされて、なかなか減らないという視点。
解き方2(総量)は、はじめにある仕事量にさらに仕事が追加されたという視点。
注目している点が違うんだ。
解き方1でも解き方2でも解けるなら、解き方1だけじゃダメですか?
今までずっと解き方1で解いてきたからなあ。
それに、今回も最後は解き方1でしたよ。
「はじめの量24」÷(12−2)=2.4(時間)
のところは解き方1でした。
よほど算数が不得意でない限り、どちらの解き方もできた方がいいよ。
解き方2でないと解けないという問題があるからなんだよ。
そういう問題を次から紹介していくよ。保護者さまへ
解き方1での式を展開して変形すれば、解き方2の式になります。
つまり、数学の目で見れば、どちらも同一の解き方になります。しかし、立式するさいの頭の使い方が異なるため、子どもの目からみればまったく別の解き方です。
