- 例題9
-
下の図は、1辺の長さが12cmの立方体です。点Q、Rはそれぞれ辺の3等分点のうちの1つです。この立方体を3点P、Q、Rを通る平面で切断します。その切断面を作図しなさい。また、切断面の図形の名前を答えなさい。
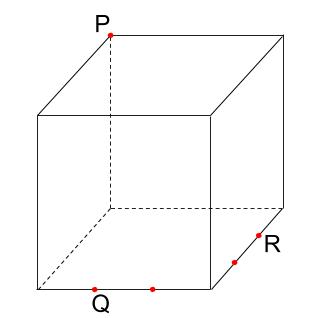
- 解説
-

「立体の切断面の切り口の作図」ルール
1.同じ平面上の点は結ぶ。
2.平行な面には、平行な線を引くまずはルール1ですね。
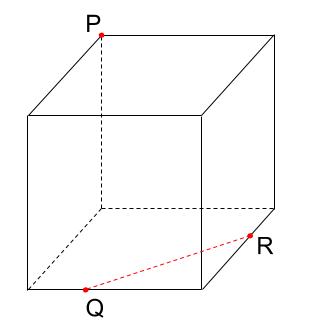

続きは・・・
ルール1もルール2も無理。ということは延長ですね・・・
どうやればいいのかな?
直線がQRしかないからね。
これを延長するしかないよ。
つまり、底面がもっともっと広かったら。
このように考えます。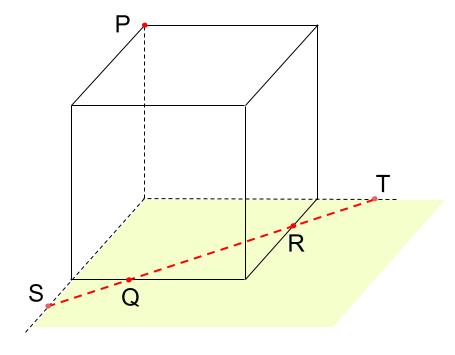

点Tは底面の上の点であり、立方体の後ろの面を延長した面上の点でもある。
つまり、点Pと点Tは同じ面上の点なのです。
ルール1によりPとTを結びます。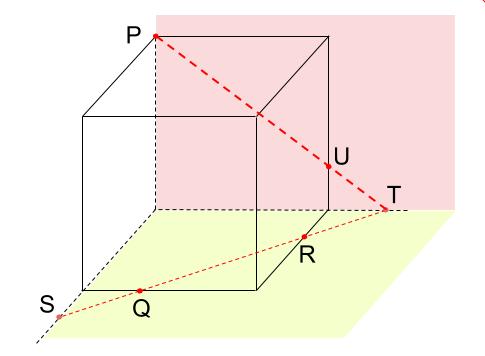

点Sは底面の上の点であり、立方体の左の面を延長した面上の点でもある。
つまり、点Pと点Sは同じ面上の点。
ルール1によりPとSを結びます。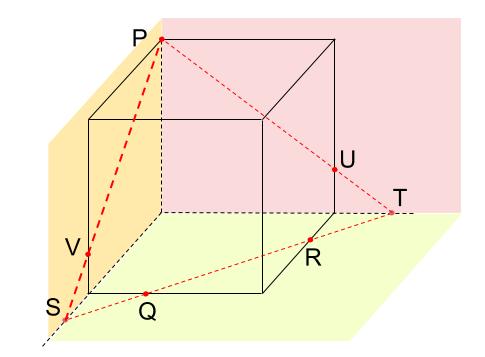

点U、Rは同じ面上の点だから結ぶ。
もちろん、URとPSは平行になっています。点V、Qは同じ面上の点だから結ぶ。
もちろん、VQとPTは平行になっています。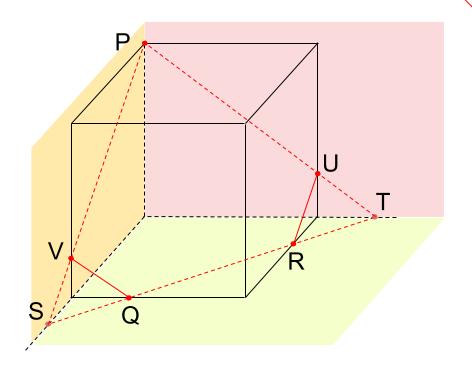

なるほど・・・!
切断面は五角形ですね。

はい、五角形ですね。
長さも求めておきましょうね。
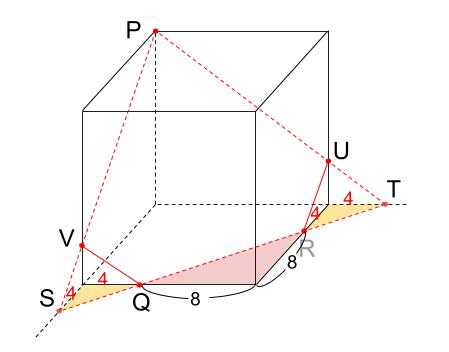

上の図で、赤い三角形と黄色の三角形は、すべて直角二等辺三角形。
それぞれ長さが求まります。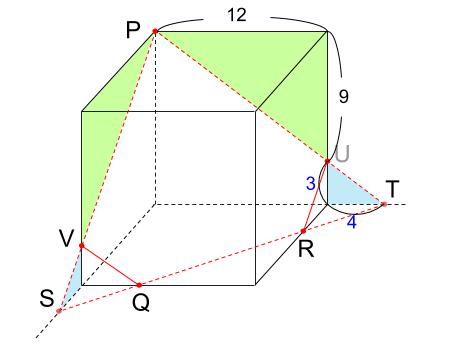

上の図で、緑の三角形と青の三角形は、相似な直角三角形。
相似比が、12:4=3:1なので、
点U、Vは、12㎝を3:1に分ける点。
9cmと3cmと、それぞれ長さが求まります。
