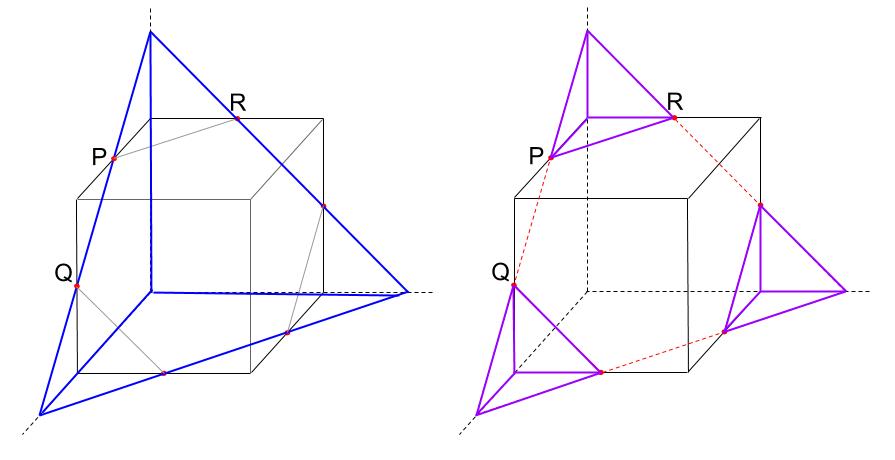
- 例題8
-
下の図は、1辺の長さが12cmの立方体です。点P、Q、Rは辺の真ん中の点です。この立方体を3点P、Q、Rを通る平面で切断します。その切断面を作図しなさい。また、切断面の図形の名前を答えなさい。
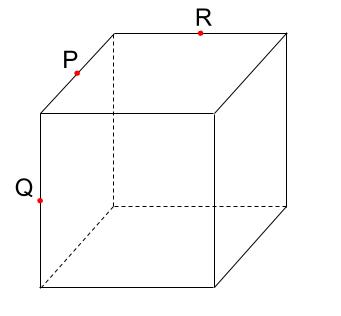
- 解説
-

「立体の切断面の切り口の作図」ルール
1.同じ平面上の点は結ぶ。
2.平行な面には、平行な線を引くまずはルール1ですね。
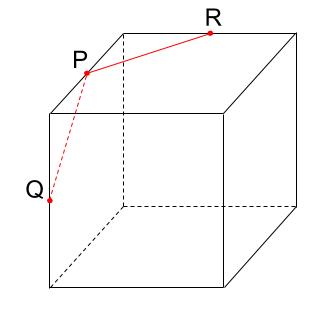

ルール1だけで解決しなかったので、ルール2を用います。
2.平行な面には、平行な線を引く
あれ?どこにも引けないぞ・・・
あれ?
はい。
とてもよくできていますよ。
今まで教えた立体切断のルールをよく学習してきてくれましたね。
で、いよいよ立体切断のルール3を教えるときがきたのです。
この問題は、ルール1と2だけでは解決できません!

え!?
ルール3?
まだ他に教えてもらっていないルールがあったんですね!!

そうなんです。
ルール3です。
そして、これが最後のルールです。
もうこれ以上ありません。ルール3、延長を考える。
です。

延長を考える・・・
なんのことだか・・・さっぱりわかりません!!
はい。
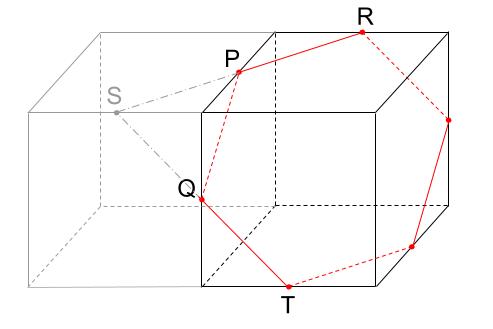
とにかくはじめは見ていてください。はじめに与えられていた立方体の左に、もう1つ同じ大きさの立方体があるとします。
PRを切ったナイフは、もう1つの立方体にも同じような切り口をつけますね。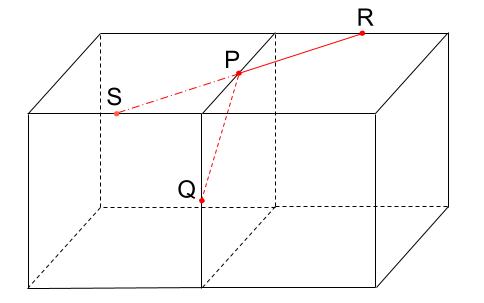

次に、前の面に注目します。
SとQは同じ面上の点です。ルール1により結びます。
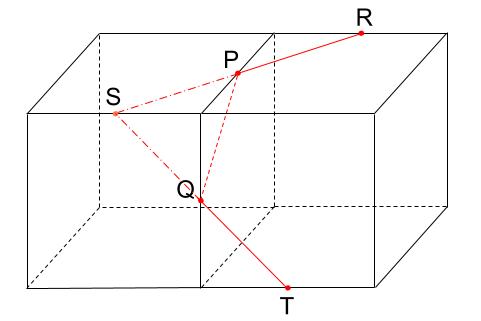

ここから先は、ルール1、2だけで解決できます。
もちろんルール3を使っても良いのですが。
ルール2ですね。
上下の面に着目します。
2.平行な面には、平行な線を引く
下図のように底面に青い線が引けますね。
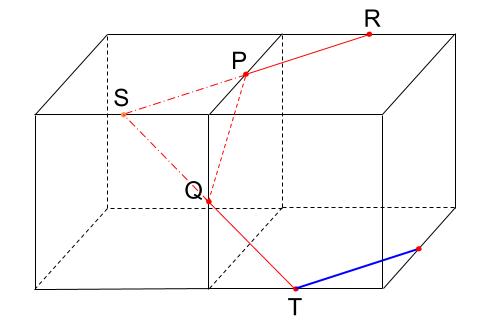

さらに、ルール2ですね。
前後の面でも、左右の面でも良いですね。
2.平行な面には、平行な線を引く
前後の面に着目すれば、緑の線が引けますね。
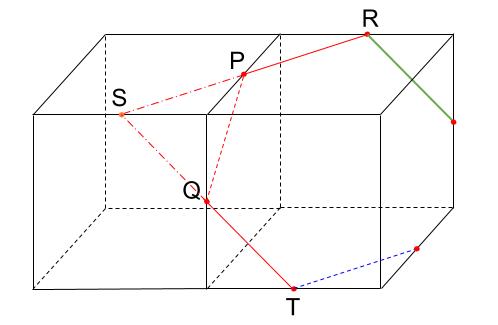

最後、ルール1。
1.同じ平面上の点は結ぶ。
右の面に、ピンクの線が引けますね。
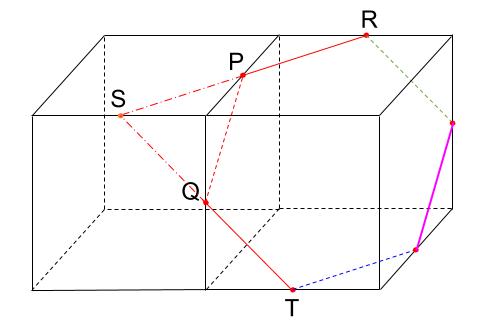

左の立方体は、本来はないものですからね。
右の立方体のみに着目します。切断面は、正六角形です。
6つの点が、すべて立方体の辺の真ん中の点になっています。

なんだか延長って難しいですね・・・

はじめはそう思うよね。
でも、とにかく練習あるのみです。すぐに、簡単だなって思うはずです。
立体切断ってワンパターンなんですよ。
さて、延長を下方向や奥の方にもするとどうなるのかを見ておきましょう。
とても大事な図ですからね。
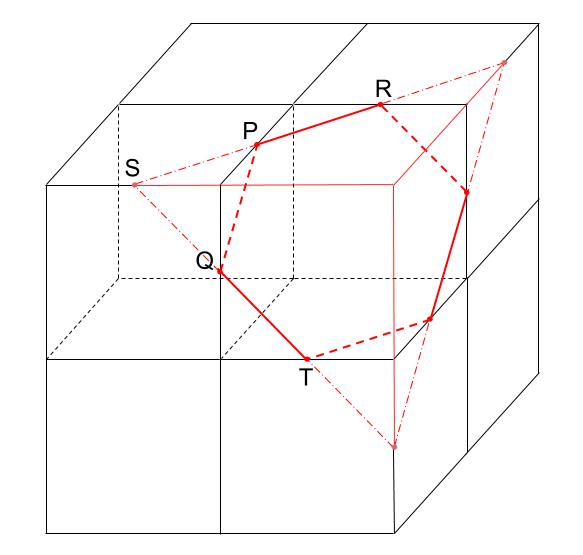

あ!正三角形の切断面の一部分なんだ。

そうだね。
そして、逆向きに延長すると下図になります。
延長するのは「面」だけで十分ですよ。
必ずしも、立方体を付け加えなくても良いのです。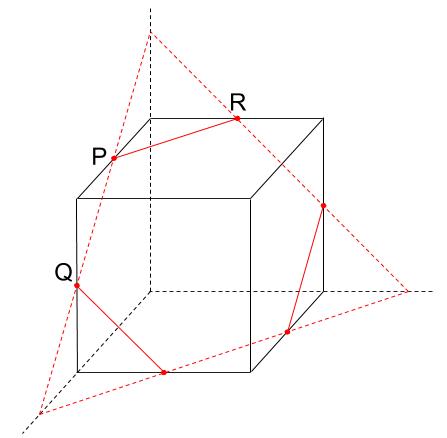

この図からは、大きな三角すいと、小さな三角すい3つが見えて欲しい。
切断はね、延長すると、必ず大三角すいと、小三角すいの組み合わせになるんだ。
大三角すいと、中三角すいと、小三角すいになることもあるし、4つの異なる大きさの三角すいの組になることもある。
これは体積の計算につながっていきます。