- 例題4
-
下の図は、1辺の長さが12cmの立方体です。点Qは辺の真ん中の点です。この立方体を3点P、Q、Rを通る平面で切断します。その切断面を作図しなさい。また、切断面の図形の名前を答えなさい。

- 解説
-

「立体の切断面の切り口の作図」ルール
1.同じ平面上の点は結ぶ。
2.平行な面には、平行な線を引くまずはルール1ですね。
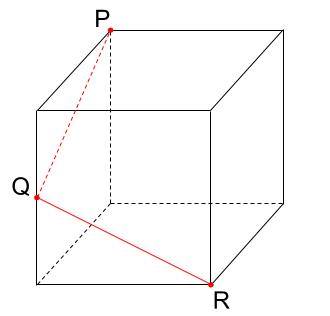

そうだね。
PとRは結ばない。
直線PRは立方体の内部をくし刺しにする直線だからね。

ルール1だけで解決しなかったので、ルール2を用います。
2.平行な面には、平行な線を引く
「左右の面」に着目して、下の青い線が引けますね。
点Sも辺の中点です。
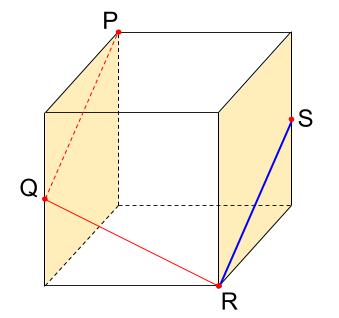

その通り。うまく解けていますね。
PQが、12cm奥に進むと6cm上にあがる直線なので、
RSも同じような傾きの直線にならないといけないわけです。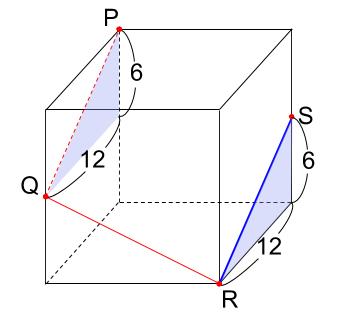

後ろの面に着目すれば、ルール1ですね。
1.同じ平面上の点は結ぶ。
ピンクの線を引いて、これで完成です!
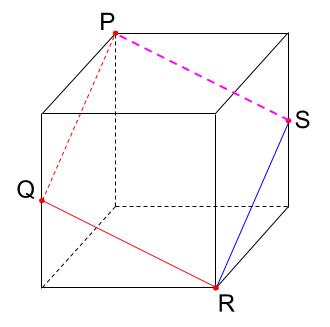

正解です!
今回ももちろん、前後の面に引かれた線は平行ですし、これを利用して作図をしてもOKです。
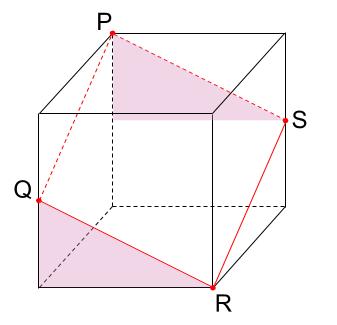

さて、この切断面の図形の名前は何かな?

平行四辺形かな。

70点かな。
100点の答えは、ひし形です。
ああそうですね。
4つの辺の長さがすべて等しいですね!下図の4つの三角形はすべて合同だから。
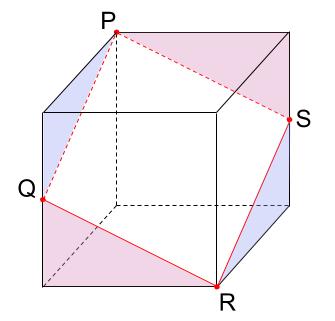

それだけだと、正方形の可能性も残っている。
この図形が正方形でなく、ひし形であることを説明するためには、対角線の長さが異なることがわかりやすいかな。
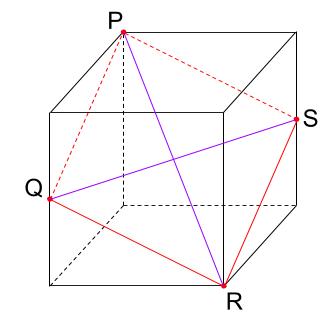

PRの方が、QSより長いですね。
なるほど!
もちろんこの2つの対角線は直交しています。
ちなみに正方形でないことの説明は、内角が直角でないことからも可能ですよ。
