【速さ】通過算・その4

またまたはじめてのパターンだね。先生が教えるよ。

通過算のポイント１・はじめと終わりの図だよ。

まずは追いつきはじめたときの図だ。
前を行く列車の最後尾に、追いかける列車の先頭が追い付いたときです。
とにかく覚えてね。

　　　　　　　　　
次に追いこし終わりの図です。

追いこし終わりの図も、はじめの図の下にかくこと。
すれ違いのときと同様だ。

そして、正確にはかけないことも同じ。
どこで追いこし終わったか、正確にはわからないからね。　　　

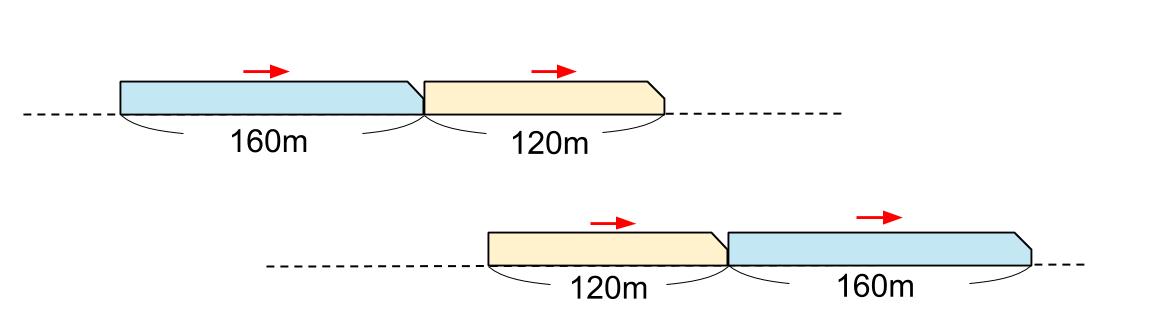
この図だけど、普通列車がちょっとしか進んでないのに追いこされているよね。
これは、追いこす方が、圧倒的に速いときの図になる。
この問題の図は、正確にかくならば、こうはならないよ。
もっともっと、時間が経過してから追いこすことになる。

なるほど。図を正確にかくことにこだわっていられませんね。

そうなんだ。

さて、　　
今回も、図のどこを見れば良いのか、ポイントがつかみづらい問題だね。
はじめての問題だし、どんどん教えてしまうよ。

さきほど、すれ違いの例題で教えた通過算のポイント３だ。
「通過が終わったときに同じ地点にいるものに着目すると良い」

今回の追いこしでは、追いこしが終わったときに、
「速い方の最後尾」と「遅い方の先頭」が同じ地点にいる。

だから下図のように、「速い方の最後尾」と「遅い方の先頭」に注目するのです。

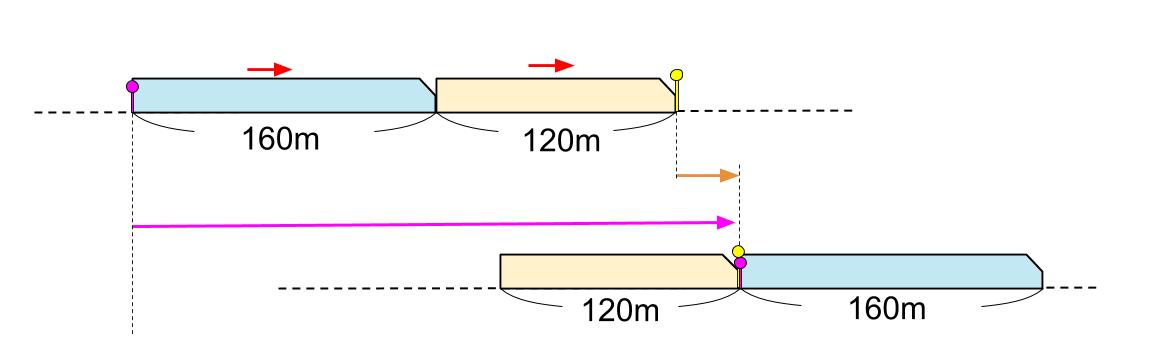
なるほど・・・
えっと・・・
あれ？どうやって解くんだこれは？？

結局は追いつきの旅人算だからね。
旅人算は、「進んだ距離の和」か「進んだ距離の差」のどちらかだったよね。

追いつきの旅人算は、たいていは差だったけど・・・

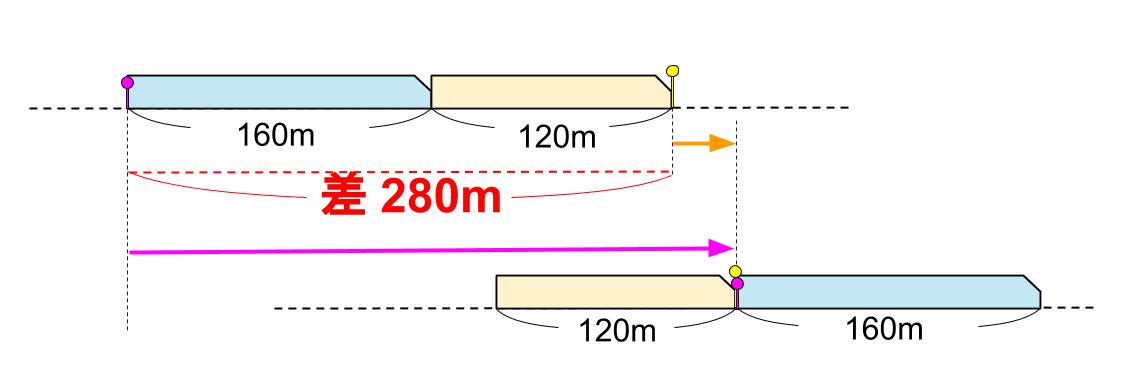
あ、進んだ距離の差が２つの列車の長さの和280mになっている！

その通り！

秒速24mの紫の人が、秒速16ｍの黄色い人に280ｍ追いつく旅人算ですね。
280÷(24－16)=35（秒）
求まりました。
35秒です。

大正解！！

この追いこしパターンも、暗記するほど何度も図をかいて練習してくださいね。