【速さ】通過算・その3

お！また新しいやつじゃないですか？

うん。これもはじめてのパターンだし、先生が教えるよ。

通過算のポイント１・はじめと終わりの図だよ。

まずはすれ違いはじめの図だ。

すれちがいはじめとは、２つの列車の先頭が出会ったときだよ。　　　　　　　　　　　　　　　　
次にすれちがい終わりの図だ
すれちがい終わりとは、２つの列車の最後尾が出会ったときだよ。　

すれちがい終わりの図はね、はじめの図の下にかくこと。
そして、正確にはかけないからそのつもりで。　

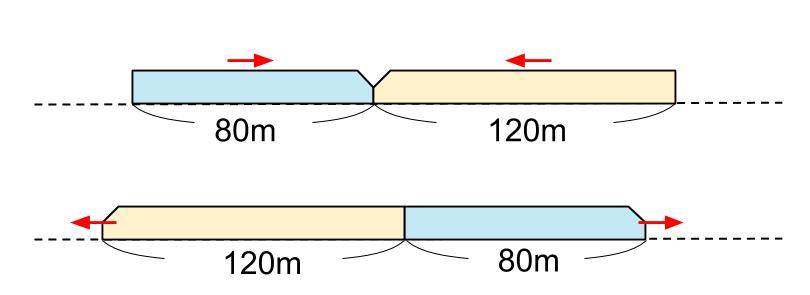
この図、正確じゃないんですか？

うん。２つの列車の最後尾が出会う地点がどこなのか、本当の地点はまだわからないよね。だからそれに関して不正確な図なんだよ。

ああ、なるほど。

続きです。
この先どうやって解いていくのか。
図を見て考えても、何がポイントなのか見えづらいんだ。

ずばり教えてしまいますね。
「２つの列車の最後尾」に着目です。

最後尾の車掌さん着目ですね。

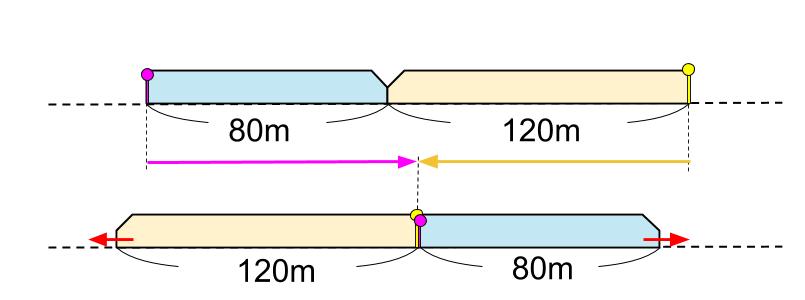
あ、出会いの旅人算だ！

2人の車掌さんは、はじめ、80+120=200（ｍ）離れてました。
で、何秒かして出会いました。そういう問題ですね。

大正解。　　
秒速25ｍと秒速15ｍで互いに近づくから、
1秒に40ｍずつ近づく。
はじめ、80＋120＝200（ｍ）離れていたから、
200÷40=5（秒）
　　　
出会ってからすれ違い終わるまで、５秒かかるのです。

なるほど、わかりました。

さっきも言ったけど、図をかいて考えても、どこに着目すべきなのか気づきにくい問題だと思う。

だから、着目ポイントは暗記しておくべきなんです。

通過算のポイント３です。
「通過が終わったときに同じ地点にいるものに着目すると良い」

今回のすれ違いでは、すれ違いが終わったときに、２つの列車の最後尾どうしが出会っている。だから、「すれ違いは、最後尾どうしの出会いに着目」となります。

ただ言葉を暗記するのではなくて、自分で何度も何度も図をかいて確かめながら暗記していきましょう。

一部うろ覚えになったとしても、図をかいて思い出せるようになることが大事です。図示を嫌がらずに練習をくり返すことなしに、確固とした基礎力はつきません。そして、図示を通してしか、理解を伴った完全なる暗記はできません。

はい。
とにかく、図示をします！