●対称 和に着目
例題1
8時と9時の間で長針と短針が、文字盤の12と6を結ぶ線分を軸として左右対称の位置になるのは8時何分ですか。
解説

えっと・・・
問題の意味がわかりません・・・

下図になる時刻を求めなさい、ということだ。
これくらい読みとれて欲しいのですが・・・


ああ、そういうことか。
で、・・・どうやって解くんだ?
8時ちょうどから動いた角度は・・・下図ですね。
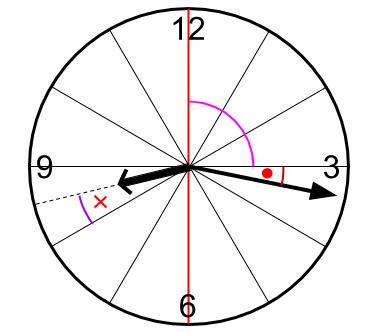

長針は、90度と赤丸だけまわった。
短針は、赤バツだけまわった。

良い図がかけてますよ。
で、今回は、12と6を結んだ直線を軸として左右対称なのだから・・・
赤丸と赤バツが下図の位置にもありますね。


なるほど・・・
で・・・わからないな。

赤丸と赤バツが今回のポイントなのはわかるよね。
何か図を見て、気がつくことがあるはずなんだけどな。

赤丸と赤バツの和が30度ですね。
文字盤の3から4までの1区間は30度だから。

その通り!!
もうこれで解けたでしょ!

長針は、90度と赤丸だけまわった。
短針は、赤バツだけまわった。
あ!
今回は、差ではなくて和なんですね!
長針と短針の回った角度の和は、120度なんだ!
(90度+赤丸)+赤バツ=90+(赤丸+赤バツ)=90+30=120
だから。

完璧ですね。
あとは計算をすれば終了です。

8時をスタート地点として、
長針と短針の回った角度の和が120度になるのは、
120÷(6+0.5)=120÷6.5=120÷\(\displaystyle \frac{13}{2}\)=\(\displaystyle \frac{240}{13}\)=18\(\displaystyle \frac{6}{13}\)
8時ちょうどの18\(\displaystyle \frac{6}{13}\)分後だから、
8時18\(\displaystyle \frac{6}{13}\)分に、2つの針は左右対称になります。

正解です!
2つの針の和に着目するんだね。
はじめてだと難しいけど、一度経験すればもう大丈夫だね!
分母が13の答えになるタイプなんだ。
