【速さ】時計算・その5

今回も時計の図をかきますね。

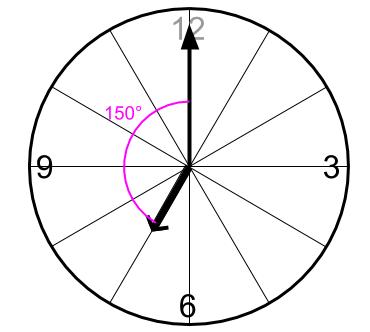
正確にはかけませんが、７時５分をすぎたあたりですね。
７時７分くらいかなあ。

はい。良い図ですよ。

今回も長針と短針の旅人算です。
旅人算のはじまりは、やはり７時０分がよいでしょうね。

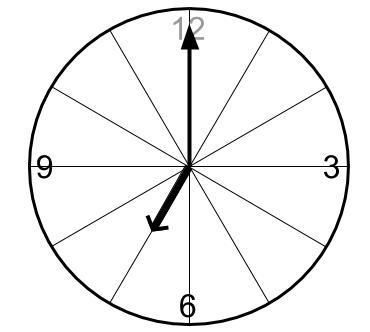
長針が短針に追いつくわけではない・・・

旅人算ですか？これ？

旅人算は、追いついたり、出会ったりするだけではないですよ。

２人の間の距離が、180ｍになるのはいつですか？
このような旅人算だってありますからね。

今回は、２つの針の間の角度が、180度になるのはいつですか？
ということです。

もう１人で解けないとまずいですよ！

７時０分に、長針は短針に210度リードされています。
このあと、長針は短針にどんどん追いついていきます。

長針と短針の差が180度になったときを求めたいので・・・

30度差をつめればよいことがわかります！

長針は１分に６度
短針は１分に0.5度
進むから、
１分で、６－0.5=5.5
5.5度ずつ追いついていく。

30÷5.5＝30÷\(\displaystyle \frac{11}{2}\)＝\(\displaystyle \frac{60}{11}\)＝5\(\displaystyle \frac{5}{11}\)　

5\(\displaystyle \frac{5}{11}\)分で長針は短針に追いつく。　

７時ちょうどの5\(\displaystyle \frac{5}{11}\)分後だから、

７時5\(\displaystyle \frac{5}{11}\)分に２つの針は一直線になります。

はい、正解です。

はじめの予想どおり、
５分から10分の間の数値が得られたから、答えに自信が持てるね。

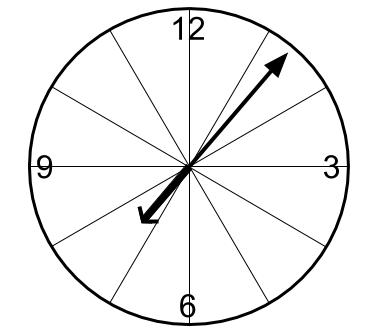
図でも確認をしておこうか。

長針が短針より30度多く回ったときに一直線になることが下図からわかるよね。

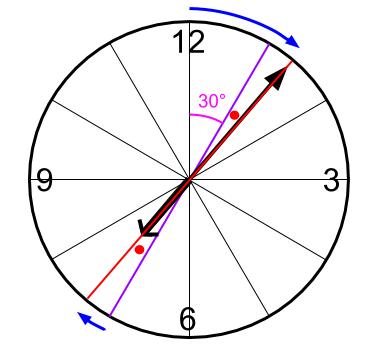
７時ちょうどをスタート地点として、

長針は、30度と赤丸の角度まわった。
短針は、赤丸の角度まわった。

２つの赤丸の角が等しいことは、対頂角だから明らかですね。
よって、長針が短針より30度多く回ったことがわかります。

あともう１つ。

様々な視点を持っておいた方が良いですからね。

リードされている長針が、短針に対して差をつめていく。
というストーリーで問題を解いたのですが、

リードしている長針が、短針に対してさらに差を広げていく。
というストーリーで問題を解くことも可能です。

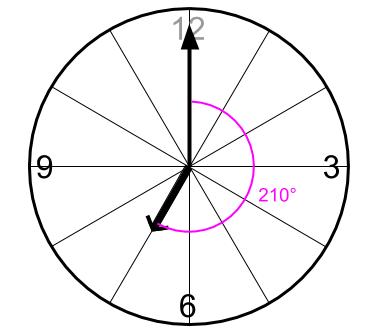
７時０分に、長針は短針に150度リードしている、という視点でも解けます。
ここから、さらに30度差を広げたときに、一直線になるわけです。