例題1
5時から6時までの間で、長針と短針のなす角が直角になるのは5時何分ですか。
すべて求めなさい。
解説

すべて求めなさい、とありますね。
1回ではないんですね。

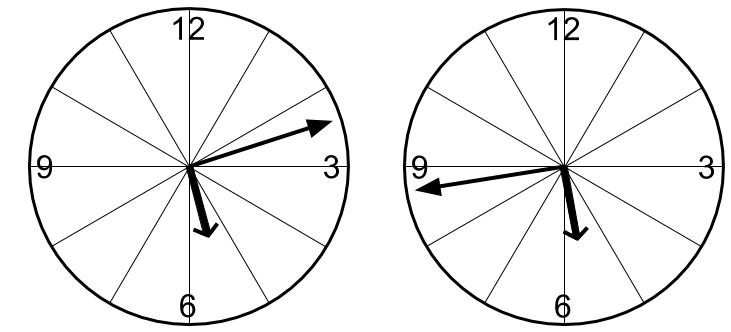
もちろん時計の絵をかいてみましょうね。

短針は5と6の間にいるのだから・・・
なるほど!直角は2回ありますね。

今回も長針と短針の旅人算です。
今までと解き方はまったく同じなので、自力で解決してくださいね。

旅人算のスタート地点は、5時0分とします。
このとき、長針は短針から150度おくれています。
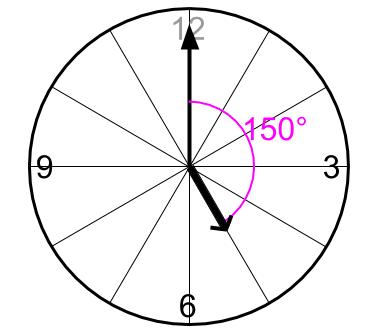

長針は短針にどんどん追いついていきます。
まず、150-90=60
長針が短針に対して60度差をつめたときに直角になります。
長針は1分に6度
短針は1分に0.5度
進むから、
1分で、6-0.5=5.5
5.5度ずつ追いついていく。
60÷5.5=60÷\(\displaystyle \frac{11}{2}\)=\(\displaystyle \frac{120}{11}\)=10\(\displaystyle \frac{10}{11}\)
10\(\displaystyle \frac{10}{11}\)分で長針は短針より、60度多くまわる。
5時ちょうどの10\(\displaystyle \frac{10}{11}\)分後だから、
5時10\(\displaystyle \frac{10}{11}\)分に2つの針は直角になります。

はい、正解です。
では、あともう1つの時刻を求めましょう!

5時0分を旅人算のスタートとして、
長針が短針よりも150度多くまわったときに、追いつく。
さらにそこから、90度リードしたときが求める時刻。
つまり、5時ちょうどからスタートして、150+90=240
長針が短針よりも240度多くまわったときに、2度目の直角になる。
240÷5.5=240÷\(\displaystyle \frac{11}{2}\)=\(\displaystyle \frac{480}{11}\)=43\(\displaystyle \frac{7}{11}\)
43\(\displaystyle \frac{7}{11}\)分で長針は短針より、240度多くまわる。
5時ちょうどの43\(\displaystyle \frac{7}{11}\) 分後だから、
5時43\(\displaystyle \frac{7}{11}\) 分に2つの針は直角になります。

はい、正解です。

ところで、ちょっとした計算の工夫なんだけどね。
まず1回目の直角を求めるために、
60÷5.5=10\(\displaystyle \frac{10}{11}\)
と計算をした。
次に、2回目の直角を求めるために、
240÷5.5
を計算することになった。
この計算は、先ほどの計算、60÷5.5=10\(\displaystyle \frac{10}{11}\)の4倍の値になるでしょ。
60÷5.5=①とすると、
240÷5.5=60×4÷5.5=④
なんだからさ。

なるほど。
ということは、
60÷5.5=10\(\displaystyle \frac{10}{11}\)だったから、
240÷5.5=10\(\displaystyle \frac{10}{11}\)×4
ということか。

そういうことです。
10\(\displaystyle \frac{10}{11}\)×4=40\(\displaystyle \frac{40}{11}\)
として、\(\displaystyle \frac{40}{11}\)=3\(\displaystyle \frac{7}{11}\) とします。
40\(\displaystyle \frac{40}{11}\)とは、40+\(\displaystyle \frac{40}{11}\) のことなので、
40\(\displaystyle \frac{40}{11}\)=40+\(\displaystyle \frac{40}{11}\) =40+3\(\displaystyle \frac{7}{11}\) =43\(\displaystyle \frac{7}{11}\)
と求めます。

あとね。
「直角になるのは、必ず1時間に2回ある」
という誤解が起きやすいから注意しておくよ。
ほとんどが2回なんだけど、1回しか起きないときもあるからね。

えっと・・・どうしてだ?
2回にならないときがある?

例えば2時?分。
2時?分に、長針と短針が直角になる時刻を求めよ。
この問いの答えは、1個しかないよ。

へえ。そうなの・・・

実際に時計の針を手動で動かしてみるのが一番わかりやすいんだけどね。
2回目に直角になる時刻が、2時60分なんだよ。
つまり、3時ちょうどに直角になります。
同様に、8時?分に長針と短針が直角になる時刻を求めよ。
この問いの答えも、1個しかないからね。

なるほど!
2回目は8時60分,つまり9時0分に直角になりますね。
