【速さ】時計算・その4

正確にはかけませんがこんな図になりますね。
何時だろう？
２時11分くらいかな。

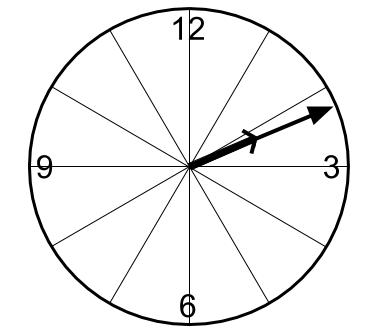
素晴らしい図だね。

でも、この図だけをじっと見ていても解けないよ。
長針と短針が動いている様子を想像して欲しい。
長針と短針は休むことなく、ぐるぐる回り続けているでしょ。
で、この図のとき重なったわけだよ。

解き方、わかったかな？

そうですね・・・・

わからないなあ。

では、ずばり教えますね。

これはね、「長針が短針に追いついた」図なんですよ。

いつ追いつきますかって問題なんだよ。

あ、旅人算だ。

そうだよ。もう１人で解けるかな？やってみよう。

旅人算のスタートは・・・？
２時ちょうどが良さそうだな。　　　

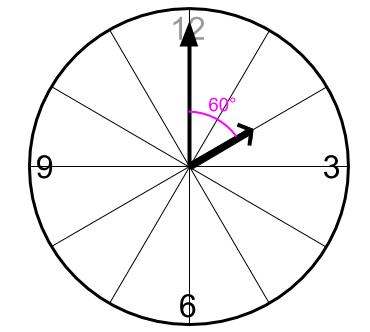
２時ちょうどに、長針は短針に60°リードされている。
そして、長針が短針にどんどん追いついていく旅人算だ。　　　　　　

長針は１分に６度
短針は１分に0.5度
進むから、
１分で、６－0.5=5.5
5.5度ずつ追いついていく。

60度おいつくのは、
60÷5.5分後・・・
　
やだな、この計算・・・
なんか間違ったかな？

いいえ、学くんの解き方でカンペキですよ。

割り切れないわり算で気持ちが悪いけど、時計算では普通のことなんだ。
もちろん分数を利用しようね。

\(60÷5.5＝60÷\)\(\displaystyle \frac{11}{2}\)＝\(\displaystyle \frac{120}{11}\)\(=10\displaystyle \frac{10}{11}\)　

\(10\displaystyle \frac{10}{11}\)分で長針は短針に追いつく。　

２時ちょうどの\(10\displaystyle \frac{10}{11}\)分後だから、

２時\(10\displaystyle \frac{10}{11}\)分に２つの針は重なります。

はい、正解です。

はじめの予想通り、２時11分くらいだったね。

最近は小学生でも、仮分数のまま答えても正解、というルールもちらほら見られるようだけどね。時計算に関しては絶対に帯分数に直したいね。

２時\(\displaystyle \frac{120}{11}\)分と言われても・・・

で、何分なの？って聞き返したくなるよね。

それに、自分のはじめの予想と大きく異なる答えが出ていないか、確かめるためにも帯分数に直した方がよいよ。

時計算は必ず帯分数！！

時計算の旅人算のはじまりはどこ（何時何分）に設定しても構いません。

どこでもよいのです。
長針と短針はどこにいるのか、正確にわかる時刻をはじまりとすれば、どこであっても計算が可能です。

上の例題では、２時０分をスタート地点として旅人算を考えました。
最も自然で、解きやすいスタート地点を選んだと言えます。

しかし、２時10分をスタート地点として旅人算を考えてもかまいません。
２時10分に長針は２を指していて、短針は２の位置から、５度まわっています。

このとき、長針は短針に５度リードされています。

この５度の差をつめるのにかかる時間は、
５÷（６－0.5）＝\(\displaystyle \frac{10}{11}\)分

２時10分の\(\displaystyle \frac{10}{11}\)分後に、２つの針が重なることが求められました。