【速さ】旅人算の導入・その3

時間が経つごとに、２人の間の距離はどうなるかな？

２人の差はどんどんひろがっていきますね。
速いほうが遅いほうを置いてけぼりにします。

うんその通り。
問題では、２人の間の距離が270mになるときを聞かれているよね。
下図のようになっています。

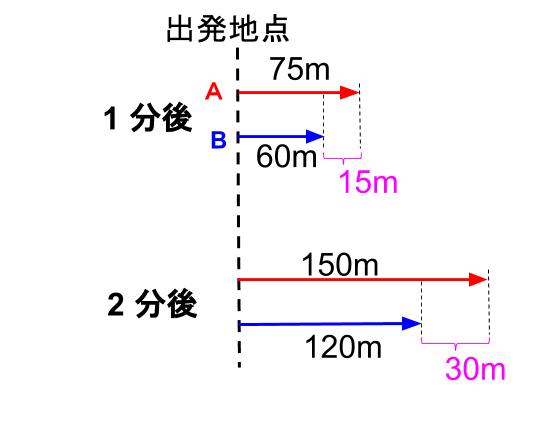
今回は差に着目なんだね。

２人の間の距離＝２人の進んだ距離の差

になっている。
いつも通りの比例関係はあるかな？

２人は１分に15ｍ離れて、２分で２倍の30m、３分で３倍の45m離れていきます。
比例します。

まったくその通りだね。

だから、２人が270mはなれるのは・・・

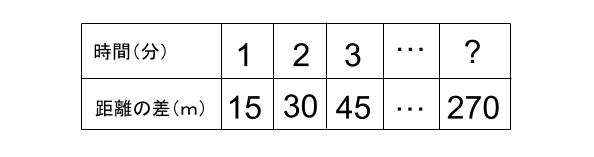
270÷15＝18

18分後です！

ばっちりだよ。
２人同時に動いているとき「２人の進んだ距離の和」も「２人の進んだ距離の差」も時間に比例するんだよ。
時間が２倍になれば距離の和（差）も２倍になる。

旅人算は、本当にただこれだけなんだ。
「２人の進んだ距離の和に着目する」のか、「２人の進んだ距離の差に着目する」のか、
どちらなのかをきちんと見極めて、あとは比例計算をするだけなんだよ。

和か差のどちらかだけ・・・
その後は比例計算。
ずいぶん単純ですね。
なんとかなりそうな気がします。

　
さて、図で２人の動きを確かめておこうか。
Ａは、75×18＝1350m
Ｂは、60×18＝1080m

1350－1080=270m

うまくいっていますね。