例題4
Aさんは分速75mで、300m先を分速60mで進むBさんを追いかけました。AさんがBさんに追いつくのは、出発から何分後ですか。
解説

Aさんの方が速いから、どんどんBさんに追いついていくよね。想像できる?

はい。
図にしてみます。
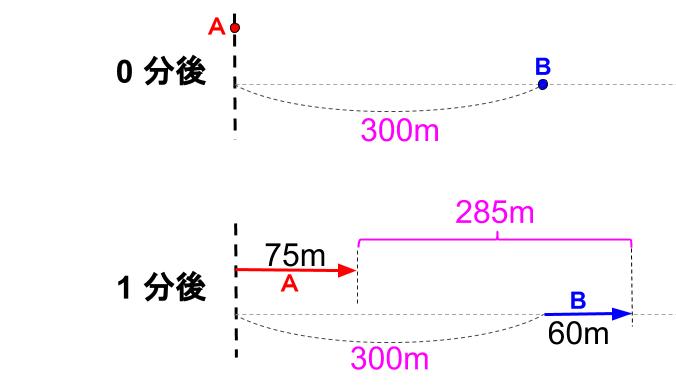

図をかくのが、けっこう難しいですね。

とてもよくかけてますよ。
ところで、続きは解けますか?

0分で300m
1分で285m
2分で270m
2人の間の距離が変化していく・・・

「2人の間の距離」に着目すると「比例」という関係はないね。
着目すべきは、
「2人の進んだ距離の和」か、
「2人の進んだ距離の差」のどちらかなんだ。
どちらなのか考えてみてね。

差かな・・・そんな気がします。
Bは1分で60m先にいくけど、Aは75m追いつくから・・・
あ!AはBに15mずつ追いつくんだ。

その通り!
1分ごとに、AはBに15mずつ差をつめる。
これがこの問題のポイントです。
旅人算では、「2人の進む距離の和」か「2人の進む距離の差」に注目して、どちらで解ける問題なのかを見極めるのだよ!
これらは必ず時間と比例するからね。

1分で15m差をつめる。
2分で30m差をつめる。
3分で45m差をつめる。
300mの差がつまるのは、
300÷15=20
20分後ですね!

大正解!
確かめもしておこうね。
Aさんは、75×20=1500m進む
Bさんは、60×20=1200m進む


うまくいってることが確かめられましたね。
ところで。
はじめに学くんがかいた図はとても素晴らしい図なのだけれど、結構たいへんだったね。
だから、「はじめから追いついたときの図」をかいて考えてしまうのがおすすめだよ。


この図を見て何がわかる?

AがBより300m多く進んだときに追いつくということがわかります。

そうだね。AはBより、1分で15m多く進むのだから、
300÷15=20
20分後と答えが求められるね。
旅人算をたくさん練習して慣れてくれば、図をかかなくたって、「AがBより300m多く進んだときに追いつく」
がすぐにわかるようになります。
今でも当たり前だって思えているかな?

300m先を行くBさんに追いつくためですもんね。
そうですね。当たり前ですね。

とにかく練習をくりかえして旅人算の基礎の基礎に慣れていこうね。
しっかり練習を積んだ後ならば、図をかかなくても基本的なことは計算だけで済ませられるようになります。
逆に言えば、しっかり練習を積む前に、図をかくことを省略してはいけないよ。
よくわからないけど計算してみました、ではまったく実力にはならないからね。
旅人算において着目すべきは、2人の進んだ距離の和で解くのか、2人の進んだ距離の差で解くのか。これをきちんと見極めること。
旅人算は「2人の進んだ距離の和で解く」、「2人の進んだ距離の差で解く」の2種類しかない。
という事実は暗記してしまって問題ありません。
出題された問題が、和と差のどちらを適用すべきなのかは、その場で自分の頭で考えて判断できるように訓練します。個々の事例を理解の伴わない暗記をしてはいけません。もちろん訓練していくうちに、出会いは和、追いかけは差、という事実は自然と暗記してしまうことになるでしょう。
しかし、出会いなのに差に着目する問題だってあります。理解を伴わない暗記は無意味なのです。
