2人の間の距離がどんどん縮まっていくパターンと
どんどん離れていくパターンがあります。
どのように変化していくかを捉えることが大切です。
1: 旅人算も正比例にすぎない
1:出会い
●2人のすすんだ距離の和タイプ
例題1
時速5㎞のAと時速3㎞のBが48㎞離れた場所から同時に出発し、向かい合わせに進みます。
2人は出発から何時間後に出会いますか。
解説

今日は旅人算と呼ばれている問題をやるよ。

旅人ってゲームみたいですね。

ゲームの中を冒険するようなやつ?
確かに日常では旅人って言葉はあまり使わないかもね。
ところで、2人が同時に動く問題が旅人算だよ。
別に旅をするわけでもないんだけどね。

2人が同時に動くって難しそうですね・・・

別に難しくないから安心してね。さっそく問題を解いてみようか。
2人が動いていく様子を図にしてみるよ。
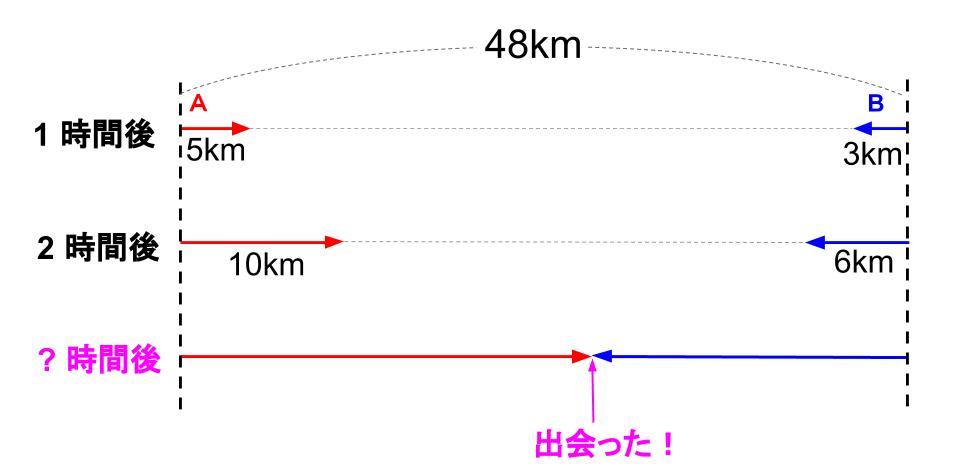

1時間で、2人は合計8km進む。
時間が2倍になれば、2人は2倍進むので、2人の進んだ距離の和は16km
時間が3倍になれば、2人は3倍進むので、2人の進んだ距離の和は24km
時間が4倍になれば、2人は4倍進むので、2人の進んだ距離の和は32km
速さの基礎でやった通り、今回も比例だよ。
この問題では、2人の進んだ距離の和=48km のときに出会うね。
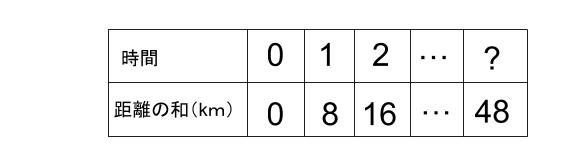

2人の進んだ距離の和=縮まる距離 が48kmになったときに出会うのだから・・・

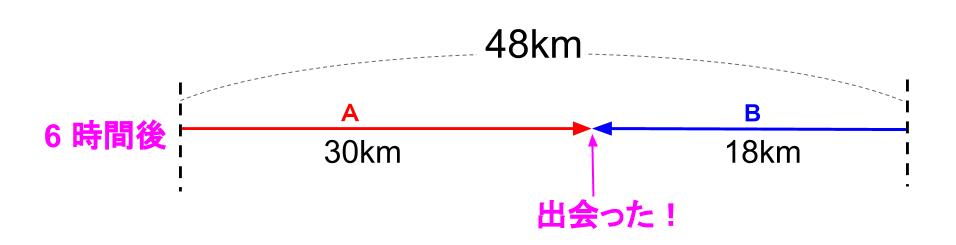
6時間後です。
(48÷8=6)

OK。その通り。確かめをしておこうか。
6時間でAは何km進むかな?
6時間でBは何km進むかな?

Aは、5×6=30km
Bは、3×6=18km
はい、2人合わせて48km進んでいます。うまくいってます。

完璧だよ!
Aが1日に5個、Bが1日に3個ずつ折り鶴を折るとして、
2人合わせて48個折り鶴を折るのは何日後かという問題と同じでしょ。

そうですね。1日に2人合わせて、5+3=8個折って、
2日で16個、3日で24個。6日で48個です。
うん、簡単です。

とにかく比例が大事なんだよ。
小学生の算数は比例を完璧に身につけることが最大の目標だからね。