1:旅人算やや応用
旅人算はとても多くの問題パターンがあります。比を使わなくとも解ける範囲での、「旅人算応用編」です。大雑把に言えば、5年生レベルの応用編です。
1:3人が登場するタイプ
例題1
Aくんは分速85mで、Bくんは分速45mで、P地点からQ地点に進みます。また、CくんはQ地点からP地点に向かって分速75mの速さで進みます。3人が同時に出発して12分後にAくんはCくんに出会いました。CくんがBくんと出会うのは3人が同時に出発してから何分後ですか。
解説
保護者さまへ
3人を同時に扱う計算方法を習ってないよー!とか言わせないでください。
そんなものはありません。3人のうち2人を選んで旅人算をするだけです。
この問題も特に何も教えずに与えて、自力でチャレンジさせたい問題です。

うわっ。3人います。
これははじめてです。習ってないです!

うん。登場人物が3人だろうが4人だろうが、特に新しく教えることはないよ。
教えることは
「今まで習ったことで解けるから安心して問題に打ち込め!」
ってことかな。

えー。そうなの・・・

うん。「まだ習ってない何かを使って解くのかもしれない、不安だな・・・」という気持ちでは全力で取り組めないでしょ。
「今まで習ったことで解ける」
という情報は、凄く重要な情報なんだよ。さあ、ガンバレ!

はい。じゃあ解いてみます。
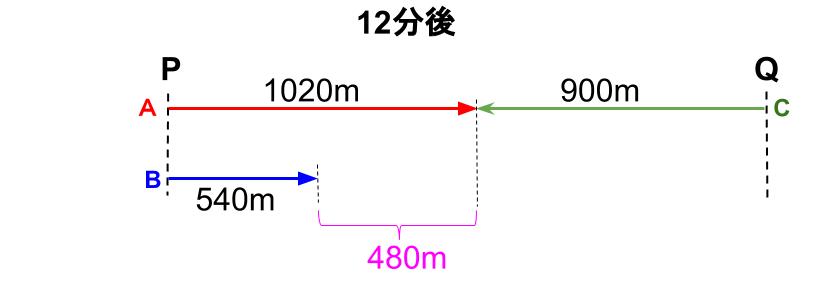
まずはAとCが出会った12分後の図かな。
A は、85×12=1020(m)
B は、45×12=540(m)
C は、75×12=900(m)
このときBとCは、1020-540=480(m)離れてる!
ここからあと何分で出会うのか、出会いの旅人算だ。

480÷(45+75)=4
4分です。

正しく解けているのだけれど、これを答案にかくと×(バツ)だな。

出発してからの時間でしたね。
12分後の、さらに4分後だから、16分です。

それで正解。
PQ間の距離が1920mと分かったから、
その間をBとCが出会いの旅人算としても解けるね。
1920÷(45+75)=16分
保護者さまへ
特に何も教えなくても、どんどん解く子は解きます。逆に、ここで手が止まる子は、解き方を手取り足取り習った問題しか解けないかなりまずい状態です。算数とは習った公式に数を入れて計算するものだと思っています。特に新しく教えることはない、もうすでにこの問題を解くために知識は教えてあるよ、といって1人立ちさせてください。3分くらいまったく手が動かずに白紙ならば、2人の情景図をかくよう声かけ。それでも手が動かないなら、1分後の図をかかせ、2分後の図をかかせ、3分後、4分後・・・とわかるまでかかせます。
