流水算
流水での旅人算の基礎
例題1
Pくんはボートで下流のA地点から上流のB地点へ、Qくんはボートで上流のB地点から下流のA地点へ同時に出発しました。AB間の距離は9kmあります。Pくんのボートの静水時の速さは時速10km、Qくんのボートの静水時の速さは時速8kmです。川の流れの速さが時速2kmのとき、PくんとQくんが出会った地点は、A地点から何kmですか。
解説

ぜんぜん難しくないから、ビビらずにやってごらん。

出会いの旅人算ですね。
Pくんは、上りだから、流速の分遅くなる。
10-2=8より、時速8km
Qくんは、下りだから、流速の分速くなる。
8+2=10より、時速10km

つまり、2つのボートは1時間で、8+10=18kmずつ近づく。
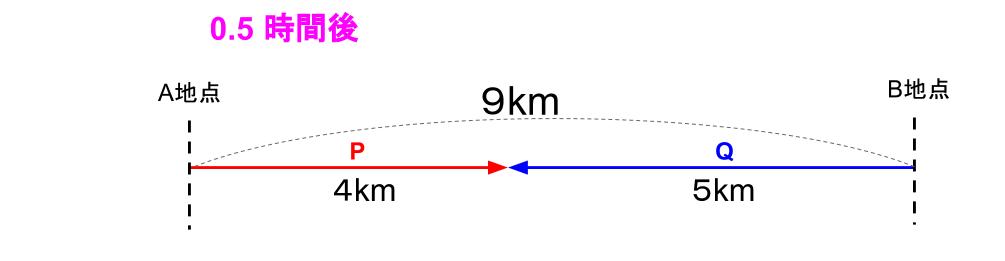
9÷18=0.5(時間)
つまり、30分。
30分後に出会います!
そして、出会うまでにPくんは、8×0.5=4
A地点から4km地点で出会っています!

大正解!きちんと解けたね!完璧。

確かに簡単でした。
流速の計算がちょっと増えただけ。簡単な旅人算でした。
例題2
PくんとQくんはボートで上流のA地点から下流のB地点へ同時に出発しました。
Pくんのボートの静水時の速さは時速10km、Qくんのボートの静水時の速さは時速6kmであり、AB間の距離は12kmあります。
PくんはB地点に着くとすぐに、A地点へ向かって引き返しました。川の流れの速さが時速2kmのとき、PくんとQくんがすれちがった地点は、A地点から何kmですか。
解説

2段階の問題ですね。
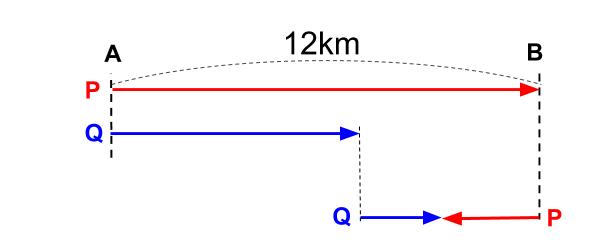
第1段階は、P君がB地点につくまで。
ここまでは、P、Qは同じ方向に進み、距離がどんどん開いていく。
第2段階は、Pが引き返してからQと出会うまで。
ここは、出会いの旅人算。

まずは第1ステージ
Pの速さは、10+2=12で時速12km
つまり、12km進むのに1時間かかる。
Qの速さは、6+2=8で時速8km
だから、1時間で8km進む。
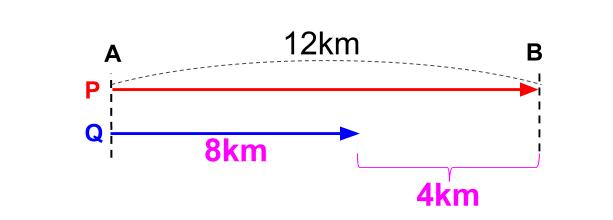

次に第2ステージ
4km離れていた2つの船が、向かい合わせに進む。
Pは折り返して上りになるから、
Pの速さは、10ー2=8より時速8km
Qの速さは、第1ステージと同じまま=時速8km
同じ速さの船が向かい合わせに進む。
もちろん、中間地点で出会うから・・・
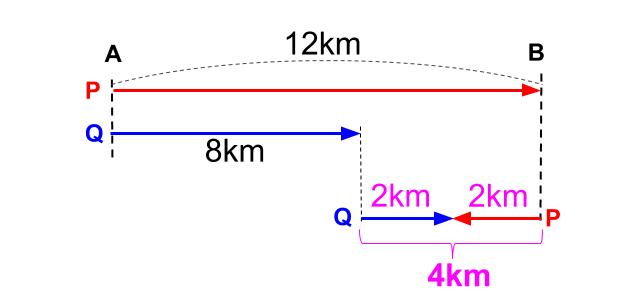

求まりました。
A地点から10㎞で出会います。

正解です!
例題3
太郎はボートで上流のA地点から下流のB地点まで、40分かけて進みました。AB間の距離は2kmあります。太郎が静水でボートをこぐときの速さは分速50m、川の流れの速さは分速15mでした。太郎はボートをこいだり、休んだりしてB地点まで進みました。休んでいる間は、川の流れの速さでボートは流されます。太郎がボートをこいだ時間の合計は何分間ですか。
解説

太郎しかでてきませんね。
出会いでも追いつきでもない・・・旅人算じゃないのかな?

とにかく情報整理をしてみるしかないよね。

こいでいるときは、50+15=65つまり、分速65m
休んでいるときは、分速15m
合計40分で、2000mを進んだ・・・
わかりました!
「速さのつるかめ算」です!
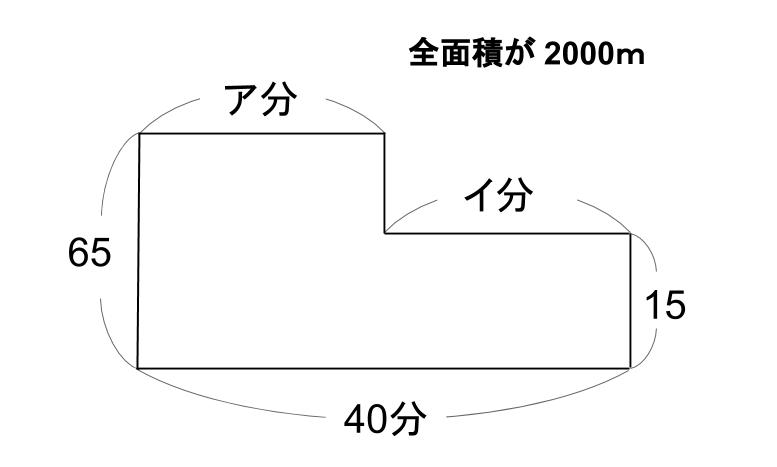

40×15=600
2000-600=1400
1400÷(65-15)=28・・・ア
求まりました。
こいでいたのは、合計28分です。

大正解!素晴らしいね。
