例題2-2
次の□に入る数を求めなさい。
分速80mで走る人は、20分で□km走ります。
解説

えーっと、80÷20=4
4kmかな・・・

あれ、なんだか自信なさそうだけど。

きっちり割り切れたし、あってます。4kmです!

ほえーーー。情けない。
私の授業をちゃんと受けていたのかい?
何も考えないで、問題に出てきた数値で適当に計算・・・
頭がすっからかんになるぞ・・・
算数は徹底的に意味を考えて、その上で計算するんだ。
重要!!!
何も考えないで、問題に出てきた数値で適当に計算する子はとても、とても多いです。特に3公式で教えられた子に多いです。そういう子は、速さに関する問題は「かけ算」か「割り算」で答えをだすという暗記をします。そしてこの問題なら、
80÷20=4
80×20=1600
の2択をします。
なんとなく数値があってそうな方を選びます・・・
そして、間違っているからやり直してね、と指導すると、何も考えずに先ほど選ばなかった方の計算をして正解をもらいます。
正解でも、まったくわかっていないという子が大勢いますので、要注意です。

速さの問題は表が大事だと教えたよね。
書いてみて。
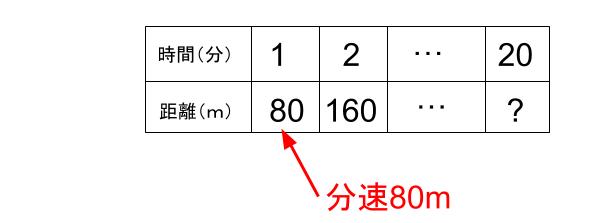

あ、時間が20倍だから、距離も20倍だ。
80×20=1600mだ。

そうだよ。この表が、速さのすべてを表しているんだ。
答えは1600m=1.6㎞となるね。
いいかげんに計算しないで、自分が何を計算しようとしているのか、きちんとわかった上で計算することが大事だよ。
速さの表をかいて整理することはとても大事だ。
しかし、最終的には表を書かないでも完璧に解ける、というレベルに到らないといけない。
そのためにも、毎回表をかいて、完璧な理解に達するんだ。
表をかいてかいてかきまくって、究めると表をかかなくてもスッと求められるようになる。
「かけ算」をすれば求まるのか、「わり算」なのか、瞬間的にわかるようになる日が来るその日まで、表をかきまくるのです。
速さとは2次元(時間と距離)の量なので、この表こそが究極に正しい理解です。

瞬間で分からないとダメですか。

そう。瞬間。
きちんと表をかいて頭を使って解いていれば、すぐにそのレベルになるよ。
学くんは1年生のころ、くり上がりの足し算とか、くり下がりのひき算とか、時間をかけて答えをだしてたろ?それが今は簡単なくり上がり、くり下がりなんて一瞬でしょ。結局はたくさん練習して慣れろってことです。

なるほど。がんばります!
ポイントは2つ
「分速80m」という言葉の意味がわかっていますか。
2倍の時間をかければ、2倍の距離を進むという関係がわかりますか。⇒比例の表
1分 20 分
80 m ?
時間が20 倍なので、進む距離も20 倍になりますね。
これが成り立つことは感覚的にも受け入れやすく、非常に簡単なタイプです。
すぐに比例の表を書くことを省略してもよいタイプの問題と思います。
3公式では
(速さ)×(時間)=(距離)
にあたる問題です。
公式から教え込むのではなく、自然に身につかせるようにしましょう。
決して公式を呪文のように、暗記するのではありません。
(速さ)×(時間)=(距離)
が成立するのは「あたりまえ」
だから自然と暗記した というプロセスを踏みましょう。
