速さと比
異なる速さで進む2人が、同じ距離を進むとどうなるのか。速さの問題の構成要素として、最重要のものの1つです。
同じ距離を進む
例題1
太郎は午前9時に家を出て、分速80mの速さで図書館に行きました。図書館で15分すごした後、分速60mの速さで家に戻ると、家に着いた時刻は午前9時50分でした。太郎の家から図書館まで何mありますか。
解説

家から図書館を分速80mと分速60mの2通りで進んでいます。
同じ距離タイプですね!
これはすぐに気づけました

うんその通り。
慣れてきたね。

速さの比は、80:60=4:3なので、かかった時間は逆比の3:4
つまり、
行き:80×③=家から図書館までの距離
帰り:60×④=家から図書館までの距離
行きに③分かかって、
図書館で15分過ごして、
帰りに④分かかった。

そうだね。
合計の時間が、
9時から9時50分までの50分だね。

つまり、③+15+④=50
より、⑦分=35分
①=5分だから、③=15分、④=20分、
行き:80×15=家から図書館までの距離
帰り:60×20=家から図書館までの距離
どちらで計算しても、家から図書館までの距離は1200mですね!

正解です。
簡単だったよね!

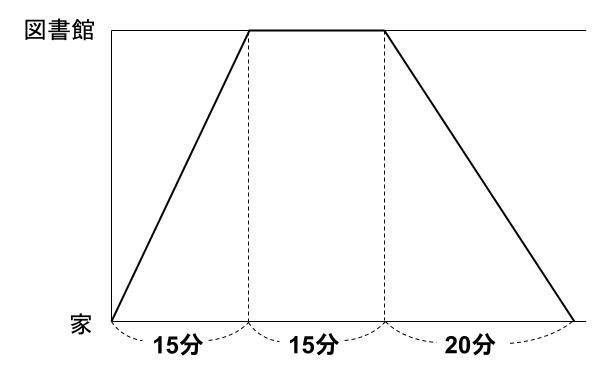
さて、この問題をダイヤグラムで見てみようか。

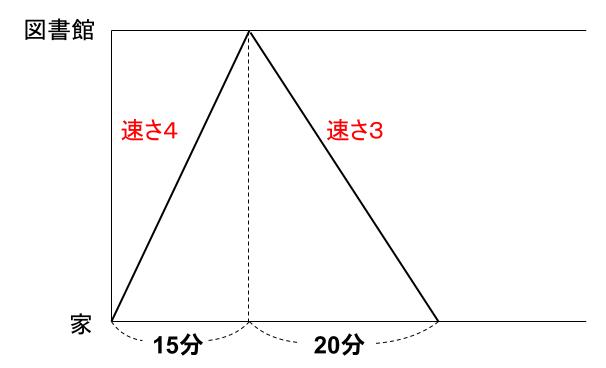
15分のストップがなければ下のようになる。
これも「同じ距離の基本の型」として覚えておこうね。
もちろん、この図から、時間の逆比がでてくるわけではないからね。
③分、④分移動にかかったことは、式処理からわかることです。

今回は時間の和から解くタイプでした。
でも大半は時間の差から解くタイプだよ。