【速さと比】同じ距離・その3

前回・前々回で学習した例題１、まだまだこの問題からたくさん学習することが残っています！

あれ？また同じ問題ですね。

まだまだ先には進まないよ。
この問題から学ぶことはとても多いからね。
次は、この問題をダイヤグラムで解いてみよう。
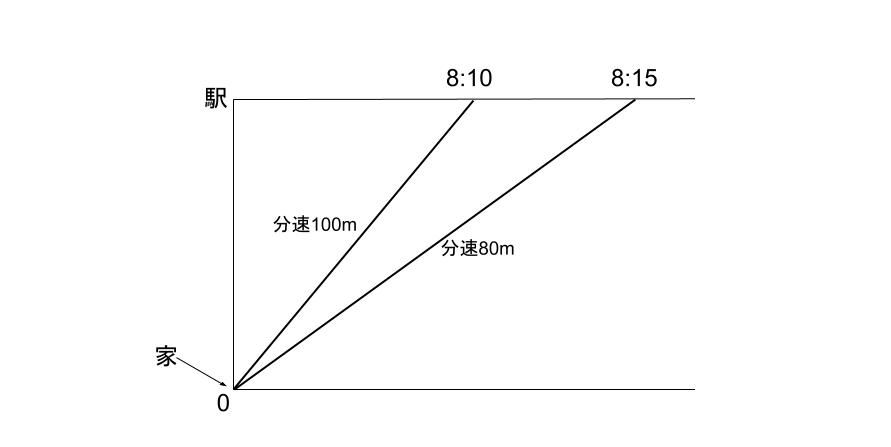
ダイヤグラムをかいてみてください。

えっと・・・苦手なんですよね。ダイヤグラム・・・

ダイヤグラムに苦手意識を持っている子は多いね。
もったいない。ダイヤグラムはとても便利な道具なんだから、使えるようにならないともったいないよ。
　　　　
とにかく嫌がらずに書く練習をやり続けること。それしかないよ。
ちなみにこの問題のダイヤグラムはかなり単純だから、かけるでしょ。

はい、こんなかな。

とても上手じゃないですか！
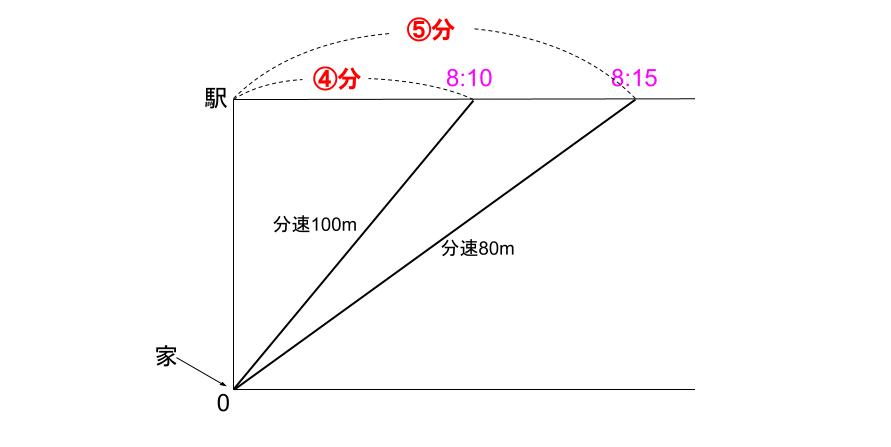
じゃあ、「同じ距離」に着目して解いていこう。
　　　　　
同じ距離を、速さ５：４で進むだのだから・・・

かかった時間は４：５ですね。

ＯＫ。しっかり覚えてくれたね。
くりかえすけども、この事実は「式から導かれる」のであって、
ダイヤグラムをかくことでわかるわけじゃない。
「式から導かれるあたりまえの事実を、ダイヤグラムの中に書きこむのです」

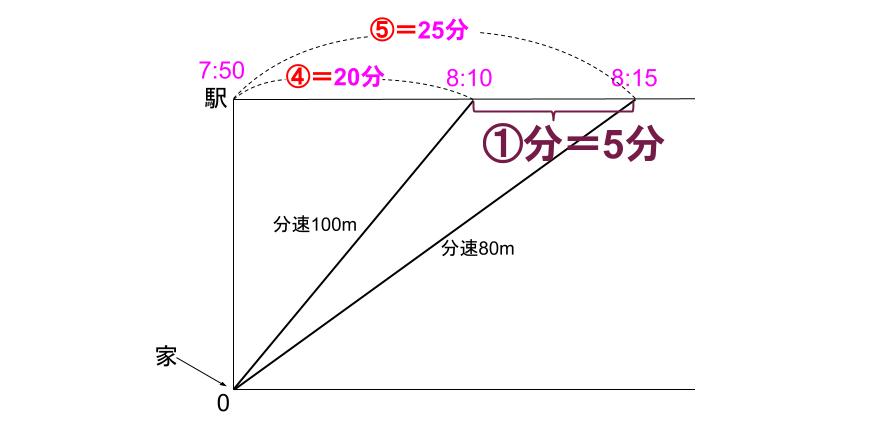
あ！①＝５がすぐわかる！
出発時刻が7時５0分もすぐわかる！
ダイヤグラム・・・便利かも・・・　

そうでしょ。
線分図は、「距離」だけを図示する図。弱点は、時刻や時間の情報が入れにくいし、見えにくいことなんだ。　
ダイヤグラムは、たて方向で「距離」、よこ方向で「時間」を図示する図。
だから、線分図の弱点である、「時間」に対しても強い。

　　
え！？じゃあ、もう線分図は卒業で、これからはダイヤグラムで解いていくんですか？

そんなことはないよ。
線分図もダイヤグラムも、両方使いこなせるというのが理想かな。
線分図はとてもシンプルに情報整理ができるからね。やはり便利な道具だよ。
たまに使いづらいときがあるから、そのときはダイヤグラムをかいて見ると良いね。

でね。このダイヤグラムも、「基本の型」として暗記してしまうことをおススメします。

「異なる速さの2人が同じ距離を進むとき、かかる時間は速さの逆比」という事実を、ダイヤグラムのどこに書きこむことになるのか、
ここまで暗記してしまいましょう。

その後、図をみながら問題を解いていくのです！