【速さと比】同じ時間・その3

複雑ですね・・・

比の活用にはまだ慣れていないから、とりあえず旅人算で解いてみようかな・・・

あれ？
旅人算では解けない？
解けないのかな、これ。

うん、旅人算では解けない。
それがわかるのが第１歩なんだ。おめでとう！

では、比で解けってことなんですかね。

そうだよ。
３つの要素のうち、２つまでは与えられているからね。
速さの問題は必ずそうなっていますからね。

図で整理します。
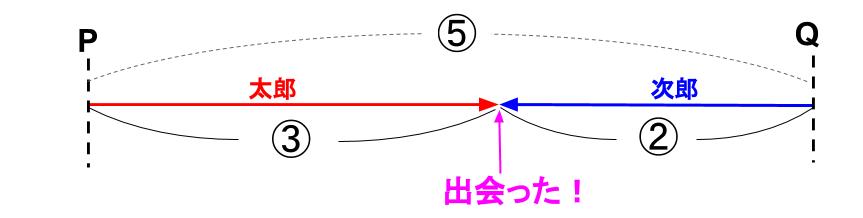
ＰＱ間の \(\displaystyle \frac{3}{5}\) の地点ですれちがったは下図。

同時に出発して出会う、旅人算的状況ですから、２人は同じ時間進んでます。
つまり、時間の比は１：１

で、進んだ距離の比は３：２だから・・・
えーっと、最後は速さだ。

速さの比が３：２だ。

うん、いいね。ここまで順調だよ。

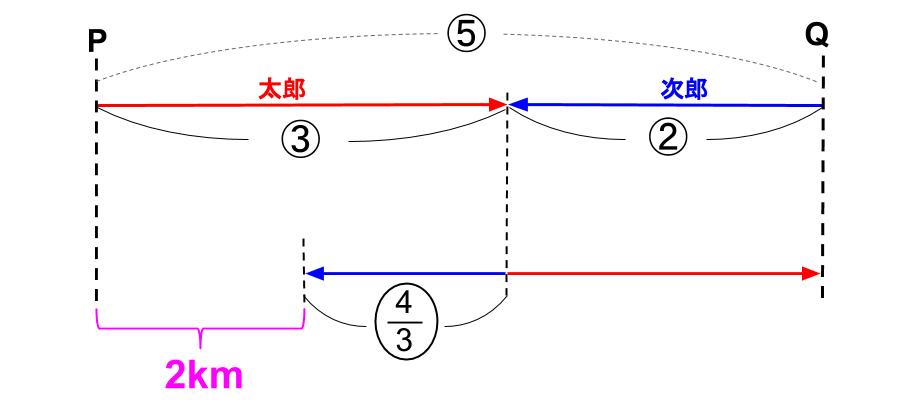
その後、太郎がＱ地点に着いたとき、次郎はＰ地点の手前２kmの地点にいた。

太郎と次郎の同じ時間に進む距離の比は３：２だから、
太郎が②進む間に、次郎は、
②×\(\displaystyle \frac{2}{3}\)＝〇\(\displaystyle \frac{4}{3}\) 進む。

できたぞ！

２kmが、③－〇\(\displaystyle \frac{4}{3}\) =〇\(\displaystyle \frac{5}{3}\) なんだ。
３倍すれば、
⑤＝６km

PQ間の距離は⑤だから、６kmだ。
求まりました！

お見事！　
完璧な解答です。

ところでちょっと別解も見ておこうか。

２人の速さの比が３：２とわかったあとなんだけどね。
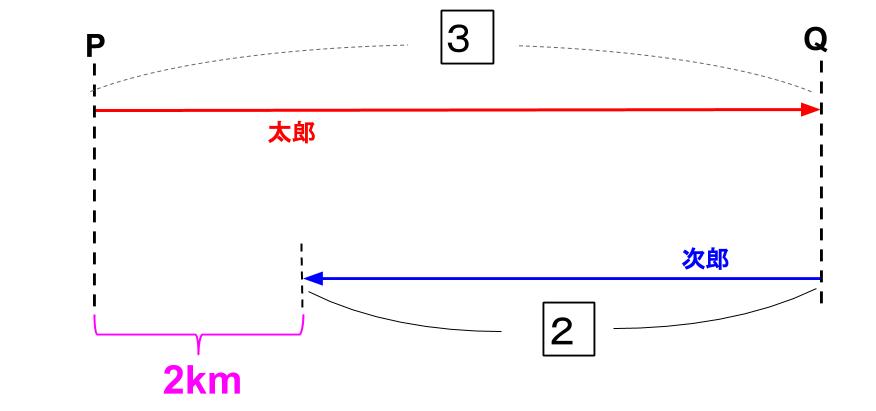
太郎がQ地点に着くまでをひとまとめで見ると下図。

速さの比が３：２の２人が、同じ時間進めば、距離の比も３：２
太郎が３
次郎が２
進んだ。
１=２ｋｍ
で、PQ間は３＝６km
なるほど！

速さの異なる２人が、同じ時間を進む問題。
まさに旅人算的状況の問題です。
これが速さの最重要パターンの１つだよ。

しっかり覚えておいてね。