速さと比・同じ時間進む
異なる速さで進む2人が、同じ時間進むとどうなるのか。速さの問題の構成要素として、最重要のものの1つです。
速さと比・同じ時間
例題2
Aくんは学校から公園に向かって、Bくんは公園から学校に向かって、午前9時に同時に出発しました。2人は午前9時10分に、学校と公園の真ん中より200m学校に近いP地点で出会いました。Aは分速80m、Bは分速96mのとき、学校から公園までの距離を求めなさい。
解説

旅人算の章で扱った問題です。
比を使わないで解くこともできますけど、比を使った方がスッキリと解けます。

この問題も、2人は同じ時間進んでいますね。
旅人算的状況は、同じ時間タイプ!覚えました。
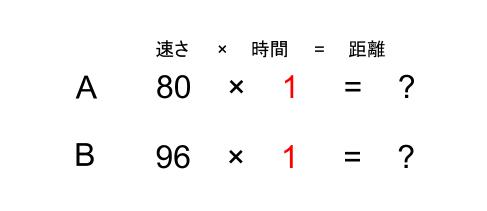
これは、速さの比と時間の比が与えられているということだ!

もちろん進んだ距離の比は計算するだけ。
80:96=5:6
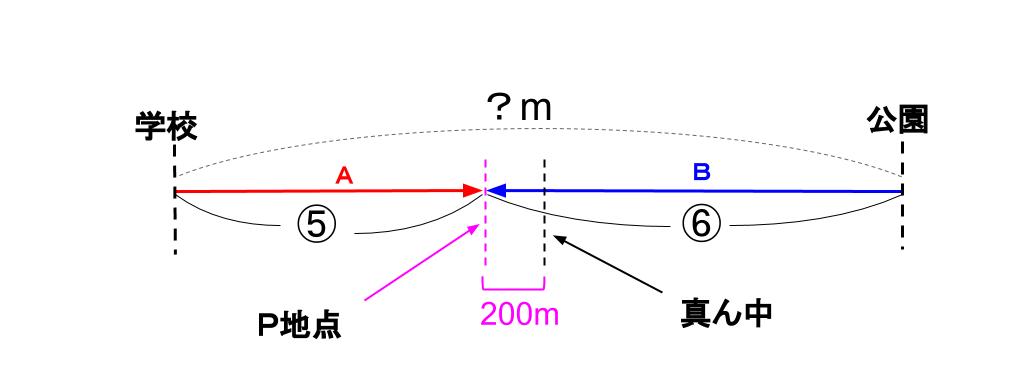
下図のようになりますね!

とてもいい図がかけたね!
あとはこの問題では、「道のりの真ん中」という話があるから・・・

学校から公園までは⑪だから、その半分は〇5.5だ!
ということは、〇0.5=200mがわかります。
もちろん、①=400m
よって、⑪=4400m
求まりました。4400mです!

正解です!
比を使うことで、2人の進んだ距離の差400mを求める必要なく解けました。
多くの子が200mと間違うやつだね。

これは確かに比で解いた方が楽ですね!
比って便利なんですね!