【速さと比】同じ速さ・その4

太郎と次郎、速さの異なる２人が400ｍを走る。
これって「同じ距離タイプ」じゃないですか。
時間の比が速さの逆比になるやつ。

（速さ）×（時間）＝（距離）　
太郎：？×80秒＝400ｍ
次郎：？×90秒＝400ｍ

まあ、そうだね。

速さの比は時間の逆比で９：８ですね。

あ！「速さの比」どころか、具体的な「秒速」がわかるぞ。

（速さ）×（時間）＝（距離）　
太郎：秒速５m×80秒＝400ｍ
次郎：秒速 \(\displaystyle \frac{40}{9}\) m×90秒＝400ｍ

聞かれているのは80秒後に次郎が、ゴールの手前どれだけにいるのか、
だから、次郎があと10秒で進む距離だ。
　　
\(\displaystyle \frac{40}{9}\) ×10＝ \(\displaystyle \frac{400}{9}\)

求まりました。
\(\displaystyle \frac{400}{9}\)= 44\(\displaystyle \frac{4}{9}\) ｍです。

まったく比を使わないで解けちゃいましたが・・・

うん。正解。
学くんの解き方で文句なし。
でも比を使うともっとあっさり解けるでしょ。

太郎と次郎の速さの比は９：８ですけど・・・

それに着目して解くこともできるけどね。
　
そうではなくて、今回比べるのは
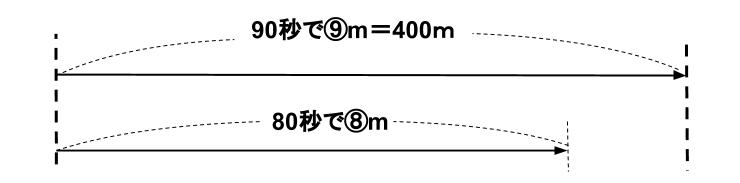
次郎は90秒で400ｍ
次郎は80秒で□ｍ
この２つ。

あ！なるほど。

時間が \(\displaystyle \frac{8}{9}\) なので、進む距離も \(\displaystyle \frac{8}{9}\) だ。

80秒のとき、ゴールまであと①mだ。

400ｍ＝⑨のときの①を求めればいい。

①＝ \(\displaystyle \frac{400}{9}\)
　　　
ほんと、あっさり求まりますね。

あらためて確認しておくけども、　
はじめの学くんの解法が悪いわけじゃないよ。
　　　
もっとも近道な解き方をしないといけないわけじゃない。
そもそも、まずは解けるようになる、ということこそが大事だからね。　
　　　
ちなみに、より近道な解法があるとして、それにどうやって気づけるようになるか。
単純で簡単な方法はないんだ。
常に問題文全体の状況を理解しようと努めるしかない。
そういう意識をもってたくさんの問題演習をすること。
全体像をいかに的確に理解、把握できるか。
これが算数における最大の力量で、一朝一夕で身に付くものではないからね。